| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Triangular Arrays
November 5, 2010
The Earth may be
round, but the world is
rectangular. That's the shape of our buildings and
nearly everything else we make. Numerical
arrays are likewise rectangular, whether business charts, data plots and the array of
pixels on your computer screen.
Triangular arrays are much less common. The most famous triangular array is probably
Pascal's triangle, which is an easy way to determine the coefficients of a
binomial equation. These are the coefficients of the terms you get when you expand the equation
(x + y)n
A physical manifestation of Pascal's triangle is
Galton's box, devised by
Francis Galton to demonstrate the normal distribution by dropping beads through an array of pegs. An interesting example of this device is seen in this
YouTube video.
I encountered another triangular array during a trip back from visiting the exhibits at the May, 1999,
Conference on Lasers and Electro Optics in
Baltimore, Maryland. Since this location was an easy day trip from our laboratory, most of my department traveled in the same van to attend. This trip is remembered more for the team camaraderie than anything we saw at the exhibits. On the way home, we stopped at a
Cracker Barrel Restaurant and were introduced to a
peg solitaire game.[1,2] Its layout is shown in the figure, and the object is to remove one peg initially, then jump pegs, as in checkers, until only one peg remains. It's actually quite difficult to do manually, so I did what any computer person would do. I wrote a solver program, which is something many others have done, and there are simulations available on the Internet.[2] I wrote my solver in Visual Basic, since I wanted to include a graphical interface, and the object code runs in my version of
Wine 1.0.1 on
Linux. It might still run on
Microsoft Windows systems, but I haven't used them since
Windows 2000, so I don't know. A zip file of the solver is available
here.
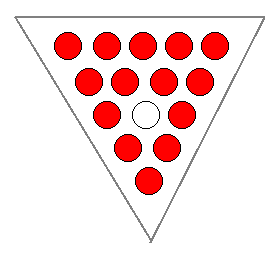
Peg Solitaire Game
Triangular arrays of objects such as pennies are easy to make, so they've been used as a teaching tool.[3] As the figure shows, the task of inverting a triangular array of pennies is an exercise in optimization. It's a fun way to introduce children to some aspects of mathematics.[3]
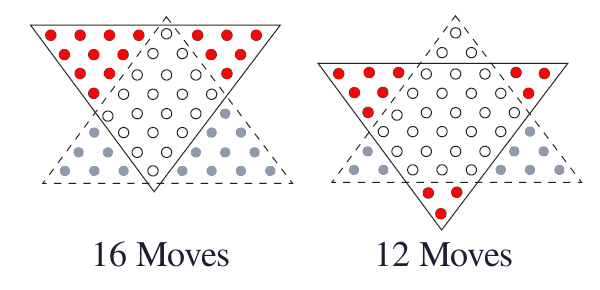
A little strategy goes a long way. Two triangle inversions from Ref. 3.[3]
An article by Jörg Pretz on the
arXiv preprint server demonstrates the use of a triangular array of lights as a binary clock display.[4,5] Jörg Pretz's version, built from bicolor LEDs, has green lights for AM, and red for PM. As he points out in his article, a clock like this is possible since the number of minutes in twelve hours (720) is six
factorial,
6! = 6 x 5 x 4 x 3 x 2 x 1
so we get our rows of 1, 2, 3, 4 and 5 elements with multipliers between the rows of 1/3, 1/4, 1/5 and 1/6, as shown in the figure. The time displayed in this example is (1 x 6 hours) + (2 x 2 hours) + (2 x 30 minutes = 1 hour) + (1 x 6 minutes) + (4 x 1 minute) = 11:10.
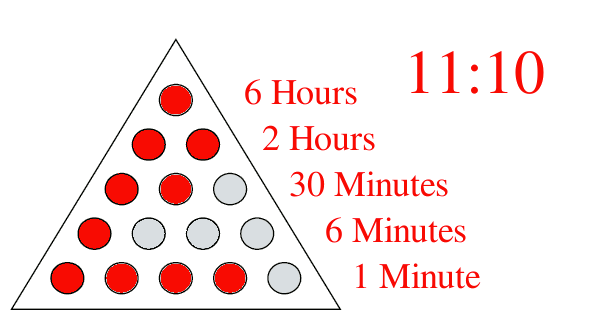
Triangular clock showing 11:10. See Refs. 4, 5.
References:
- Dan O’Brien, Peg Board Puzzle Solution Page
- Cracker Barrel Triangle Puzzle
- Arthur J. Baroody and Jesse L. M. Wilkins, "Inverting a Triangular Array: Involving Students in Mathematical Inquiry," Mathematics Teaching in the Middle School, vol. 9, no. 6 (February, 2004), pp. 306-313.
- Jörg Pretz, "A different way to read off the time - A new idea for a binary clock," arXiv, June 7, 2010.
- Jörg Pretz, Binary Clock Web Site.
Permanent Link to this article
Linked Keywords: Sphere; rectangle; doughnut; arrays; pixels; triangular arrays; Pascal's triangle; binomial equation; Galton's box; Francis Galton; Conference on Lasers and Electro Optics; CLEO; Baltimore, Maryland; Cracker Barrel Restaurant; peg solitaire; Wine 1.0.1; Linux; Microsoft Windows; Windows 2000; arXiv preprint server; factorial.