Thales, Heron, and Experimental Mathematics
February 12, 2024
Euclidean geometry was
taught to
my generation during the
sophomore year of
high school. There was even the
argument in those days that the
logical reasoning involved in
geometrical proofs was worthwhile in its own right, independent of whether the geometry used would be
useful in later life. Geometry was very important in my later
scientific life; but, for others, probably not at all.
My
interest was especially
excited by two things learned at that time. One of these was
Thales's theorem, named after the
Greek philosopher,
Thales of Miletus (c. 624 - c. 546 BC). Thale's theorem states that any
angle inscribed in a
semicircle is a
right angle. Thales was one of the first Greek philosophers interested in
physics. Unfortunately, his work is known to us only through the works of other philosophers, including
Aristotle.
The other thing of interest to me was
Heron's formula, named after
Heron of Alexandria (c. 10 - 70 AD), a
Greek mathematician,
engineer, and
native of
Alexandria in
Roman Egypt in the
1st century. Heron's formula gives the
area of any
triangle as a
function of the
lengths of its
sides. It's quite likely that Heron didn't discover this formula, which is included in his
Metrica, but his name is linked to it, nonetheless. I wrote about Hero's many
inventions in a
previous article (Steam Power, January 28, 2011). The most famous of Heron's inventions, his
steam engine, called an
Aeolipile, was published in his book,
Pneumatica. Heron's steam engine, although primitive, predates
James Watt by seventeen
centuries.

Left, Heron of Alexandria (c. 10 - 70 AD), and right, Thales of Miletus (c. 624 - c. 546 BC). (Left image, an illustration from the Codex of San Gregorio de Nizance, a ninth century Greek manuscript, from Wikimedia Commons. Right image, a woodcut from the Nuremberg Chronicle (1493), also from Wikimedia Commons.)
Aristotle tells an interesting
anecdote about Thales in his
Politics.
"He was reproached for his poverty, which was supposed to show that philosophy was of no use. According to the story, he knew by his skill in the stars while it was yet winter that there would be a great harvest of olives in the coming year; so, having a little money, he gave deposits for the use of all the olive-presses in Chios and Miletus, which he hired at a low price because no one bid against him. When the harvest-time came, and many were wanted all at once and of a sudden, he let them out at any rate which he pleased, and made a quantity of money. Thus he showed the world that philosophers can easily be rich if they like, but that their ambition is of another sort."[1]
The
proof of Thales's theorem is illustrated in the following figure.
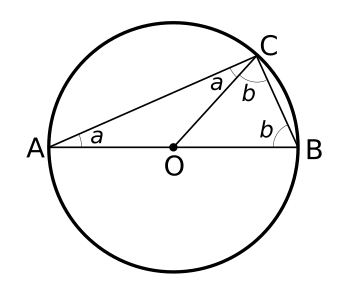
Proof of Thales's theorem.
Since the circle radii are equal, two isosceles triangles can be formed.
Thus, ∠BOC = (180-2b), ∠AOC = (180-∠BOC) = 2b, 180 = 2(a+b), and (a+b) = 90.
(Created by the author using Inkscape
A proof such as this is the
mathematical gold standard; but, how would you convince yourself that a proof is likely and worthy of your effort? That's where
experimental mathematics can be used as a tool. While a Thales's
conjecture is easy to
validate using a
computer program, other conjectures do not appear as obvious, and recourse to experimental mathematics could save needless effort. I've created a simple
C language program (
source code here) that creates
random inscribed triangles in a semicircle and tests the validity of the
converse of the
Pythagorean theorem; that is, that the
square of the longest side, in our case, the
diameter, is equal to the sum of the squares of the other two sides. For a circle of
radius 1, the
mean diameter after a million trials is 2.000000±0.
Heron's formula for the area
A of a triangle with sides
a,
b, and
c, is simply,
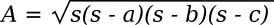
Where
s, known as the
semiperimeter, is half the
perimeter; viz.,
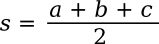
The formula can be written in terms of the sides, only, as
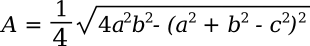
Checking the validity of Heron's formula for a
scalene triangle simply involves decomposing the triangle into two
right triangles (see figure) and comparing the sum of their areas to the area given by the formula. I've created a simple C language program (source code
here) that does this. For 100,000 trials, the difference of the two values was -0.000001±0.000099, the slight error attributed to
floating point precision.
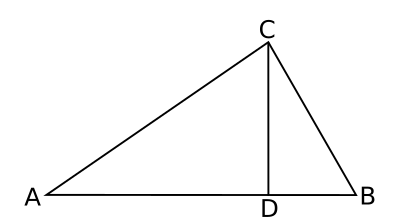
Scalene triangle decomposed into two right triangles.
(Created by the author using Inkscape
![]()
Reference:
- Aristotle, Politics, Book I, Part XI, via MIT Classics.
Linked Keywords: Euclidean geometry; education; taught; baby boomer; my generation; sophomore yea; high school; argument; logical reasoning; geometry; geometrical; mathematical proof; utility; useful; science; scientific; point of interest; pleasure; excited; Thales's theorem; ancient Greek philosophy; Greek philosopher; Thales of Miletus (c. 624 - c. 546 BC); angle; semicircle; right angle; physics; Aristotle; Heron's formula; Heron of Alexandria (c. 10 - 70 AD); Greek culture; Greek; mathematician; engineer; native; Alexandria; Roman Egypt; 1st century; area; triangle; function (mathematics); length; edge (geometry); side; invention; steam engine; Aeolipile; James Watt; century; centuries; illustration; Codex; ninth century; Greek language; manuscript; Nuremberg Chronicle (1493); anecdote; Politics (Aristotle); reproach; poverty; philosophy; astrology; skill in the stars; winter; harvest; olives; money; deposit (finance); olive-presses; Chios; Miletus; price; bid price; wealth; rich; ambition; circle; radius; radii; isosceles triangle; Inkscape; mathematics; mathematical; gold standard (test); experimental mathematics; conjecture; validity (logic); validate; computer program<; C language program; source code; thales.c; randomness; random; inscribed figure; converse (logic); Pythagorean theorem; exponentiation; square; diameter; average; mean; semiperimeter; perimeter; scalene; right triangle; heron.c; floating point; significand; precision.