| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Rubik's Cube
August 27, 2010
Symmetry is used to simplify many problems. One of the most fundamental mathematical symmetries that's useful in the physical sciences is the concept of
odd and even functions. Knowing that the functions you are analyzing are odd or even leads to many simplifications, the most useful of which involves integration. The integral of an odd function from -x to +x is zero, provided that there is no vertical
asymptote in that range. Likewise, the integral of an even function from -x to +x is twice the integral from 0 to +x (same caveat about an asymptote).
Symmetry is useful in some unexpected places. A family member once purchased a
Rubik's Cube puzzle for me at a garage sale. Unlike store-stocked cubes that are packaged as a "solved" cube with each face showing a single color, this cube was scrambled. The faces of this cube were colored by attachment of vinyl squares to the plastic mechanism. I immediately realized that this cube puzzle wasn't solvable, since someone had swapped some of the colored squares. A corner element on this particular cube had the same color on two faces. Since a solved cube has a different color on each face, there was no possible manipulation of the cube that would do this.
I wrote about Rubik's Cube in a
previous article (Rubik's Cube, April 11, 2008). There's a lot of mathematics in the Rubik's cube puzzle. The cube has its own
mathematical group that corresponds to the set of all possible operations. Because of the plethora of initial states that a cube can have, this group has 43,252,003,274,489,856,000 elements; or, more descriptively,
2273145372111

Rubik's Cube.
Mathematical analysis of Rubik's Cube began quite soon after it was introduced. The main question on everyone's mind was the minimum number of operations it takes to solve an arbitrary cube. There are quite a few known
algorithms for "solving" the Cube that take fewer than a hundred moves. Notice the quotation marks around "solving." These operations work, but they are not proven to
always work. Rubik's Cube was introduced in America in 1980, and computing at that time was not sufficiently developed to analyze all positions of the cube and state with surety the minimum number of operations for solution. In 1981, the mathematician,
Morwen Thistlethwaite, showed that at most 52 moves would suffice. Over the years, this number was reduced, [1] and in 2008 it was known that 22 moves will suffice. That number was found by Tomas Rokicki and John Welborn. [2] Rokicki, a programmer from
Palo Alto, CA, continued to work on the problem with Morley Davidson, a mathematician from
Kent State University, John Dethridge, an engineer at
Google in
Mountain View, CA, and Herbert Kociemba, a mathematics teacher from
Darmstadt, Germany.
In July, 2010, this team announced via their web site,
http://www.cube20.org, that they had analyzed every Rubik's Cube position by computer and found that
no more than 20 moves suffice. The analysis consumed 35 CPU-years of idle computer time donated by Google. Their method, according to their web site,[1] was as follows:
• They partitioned the positions into 2,217,093,120 sets of 19,508,428,800 positions each.
• They reduced the count of sets needed to solve to 55,882,296 using symmetry and set covering.
• They didn't attempt to find optimal solutions to each position, but instead only solutions of length 20 or less.
• Their program solved a single set in about 20 seconds.
• It would take a four-core, 2.8 GHz computer 1.1 billion CPU-seconds, or 35 CPU years, to find solutions to all of the positions in each of the 55,882,296 sets. [3]
The graph of the required number of moves needed to solve Rubik's Cube is interesting. Of course, there is only one configuration that requires zero moves, and things are quite uniform on a logarithmic scale until close to the twenty move limit. As the team demonstrated, there are no configurations that require more than twenty moves to solve.
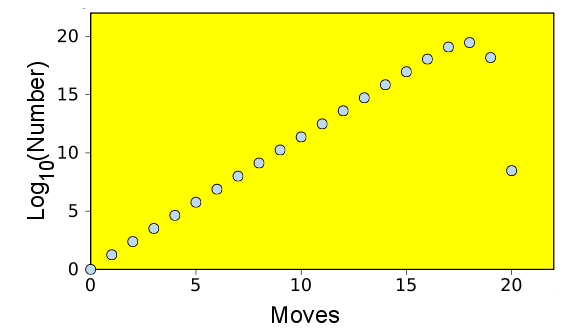
This work reminds me of the computer-assisted proof of the
Four-Color Conjecture that I wrote about in a
previous article (You Can Get There From Here, March 26, 2008). The conjecture, that you need only four colors to color a map such that no adjacent regions have the same color, was not easy to prove analytically. In 1976,
Kenneth Appel and
Wolfgang Haken published a proof of this conjecture using a computer to analyze every conceivable map.
References:
- Tomas Rokicki, "Twenty-Five Moves Suffice for Rubik's Cube" (ArXiv, March 24, 2008)
- The Cube-20 Web Site
- Surprisingly, this amounts to less than $10,000 of supercomputer time.
Permanent Link to this article
Linked Keywords: Symmetry; odd and even functions; asymptote; Rubik's Cube; mathematical group; algorithms; Morwen Thistlethwaite; Palo Alto, CA; Kent State University; Google; Mountain View, CA; Darmstadt, Germany; http://www.cube20.org; Four-Color Conjecture; Four-Color Theorem; Kenneth Appel; Wolfgang Haken.