Quantum Random Numbers
September 27, 2010
One of my interests is
random numbers. My critics may claim that this is obvious from my published data. If perfect data were too easy to obtain, they wouldn't pay us so much money for our research, a fact that I stated when I was interviewed by
Ed Wallace for a post-doctoral position many years ago. I mentioned in a
previous article (Random Computing, July 26, 2010) that I was building a random digit display using
white noise in analog circuitry at the same time that
men first landed on the moon. This was a physical random number generator; that is, the random numbers came from a random natural process, and not from a computation. Such physical generators are harder to implement, but they're preferred for the obvious reason that a computed random number is not really random. As
John von Neumann so famously stated,[1]
Any one who considers arithmetical methods of producing random digits is, of course, in a state of sin.
Researchers at the
Max Planck Institute for the Physics of Light (Max-Planck-Institut für die Physik des Lichts) in
Erlangen, Germany, have gone to the ultimate source for their random numbers; namely, the seething undercurrent of
quantum foam known as the
vacuum state. Their apparatus is quite simple. An intense laser beam from a 1.500 nm
distributed-feedback laser is split into two beams by a
beam splitter, and the two beams are separately detected and compared. One beam, however, is mixed with noise from the vacuum states, as shown in the figure.
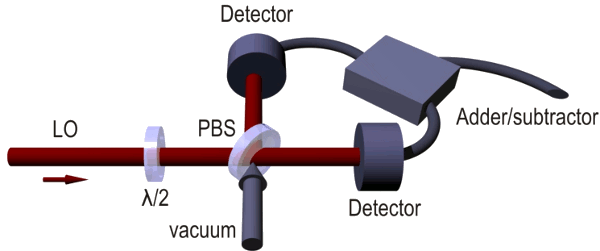
Apparatus for measuring random vacuum states (Max Planck Institute).
The beam splitter in this case is the combination of the
half-wave plate and a polarizing beam splitter (PBS). This allowed a precise 50-50 adjustment of the detector amplitudes. In the absence of the vacuum fluctuations, the amplitude of voltage at each detector is the same, so subtracting them will give zero. Add in the vacuum states, and the subtraction gives the quantum noise.
The only problem with this device is the fact that the electronics has its own
noise component that's mixed with the quantum noise. As a consequence, the raw data fails 54% of a suite of tests for randomness; namely, 75 out of 139 tests of the Crush test battery.[4] When the
SHA-512 hash algorithm is applied as a "whitening" function, the electronic noise is effectively removed, and all random tests in the Crush suite are passed. The rate of random bit generation with this particular optical circuit was about 6.5 Mbit/second. The authors think that 200 Mbit/second is not a problem in a better apparatus, and this would translate to about 400,000 516-bit numbers per second. Not very speedy, but certainly unique. As I mentioned in a
previous article (Random Computing, July 26, 2010),
Intel researchers have built a random number generator that produces billions of random bits per second.
The Max Planck Institute research group has placed files of 516-bit random numbers on the Internet.[5,6] So, what does a computer person do when he sees something like this? He checks for himself. I wrote a C program that extracts the four least significant bytes of 100,000 of the 32 byte data records as
unsigned integers, and I analyzed them using
Gnumeric. The resulting histogram is shown below. Sure, it's not very scientific, but
a picture is worth a thousand words. Actually, a hundred thousand 32-bit words in this case.
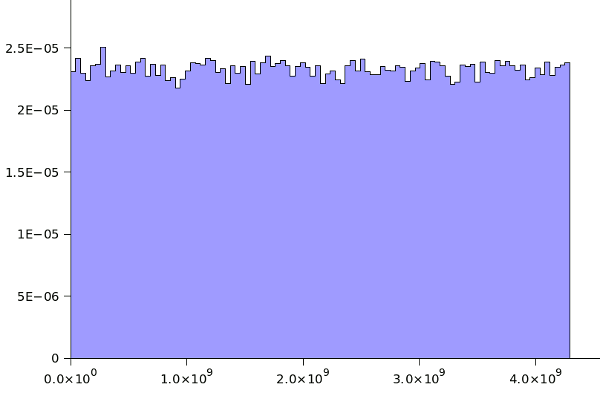
Histogram of 100,000 quantum random numbers.
References:
- Quotations of John von Neumann on Wikiquote.
- Random numbers game with quantum dice, Max Planck Society Press Release C/2010(203), September, 2010.
- Christian Gabriel, Christoffer Wittmann, Denis Sych, Ruifang Dong, Wolfgang Mauerer, Ulrik L. Andersen, Christoph Marquardt and Gerd Leuchs, "A generator for unique quantum random numbers based on vacuum states," Nature Photonics,doi:10.1038/nphoton.2010.197, August 29, 2010.
- P. L'Ecuyer and R. Simard, "TestU01: A C library for empirical testing of random
number generators," ACM Trans. Math. Software, vol. 33, no. 4 (2007) p. 22. Source code available here.
- 50 MB binary file of 512-bit random numbers.
- 200 MB binary file of 512-bit random numbers.
Permanent Link to this article
Linked Keywords: Random numbers; William E. Wallace; Ed Wallace; white noise; Apollo 11; John von Neumann; Max Planck Institute for the Physics of Light; Erlangen, Germany; quantum foam; vacuum state; distributed-feedback laser; beam splitter; half-wave plate; electronic noise; SHA-512 hash algorithm; unsigned integer; Intel; Gnumeric; a picture is worth a thousand words.