Packing
November 30, 2010
The arrangement of
pennies on a
plane that gives an optimal packing (most pennies per area) is so trivial that it's
nearly instinctive. You arrange them such that their centers are on an
hexagonal lattice. This optimal lattice packing of circles on a plane was proven mathematically by
Carl Friedrich Gauss, and the resultant density is (π/2√3) = 0.9069.[1] In 1940,
László Fejes Tóth showed that this is the optimal packing, lattice or otherwise.[1] We can still obtain compact packing when the coins are of different size, as shown in the figure. In this case, the coins have diameter 1 and the
root of the equation, r
4 - 10r
2 - 8r + 9.[2]
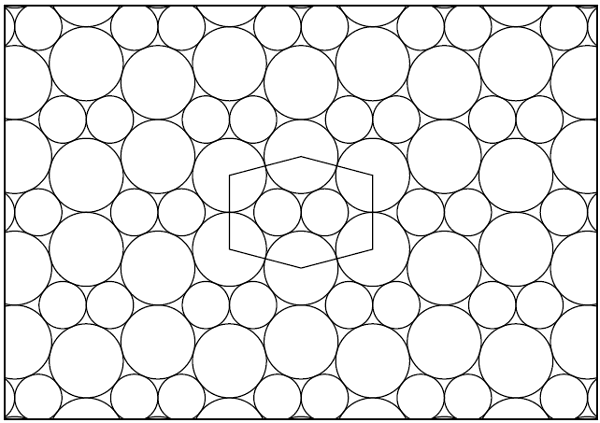
Compact packing of two sizes of disks of radius 1 and 0.6375559772... Figure 1 of Ref. 2.[2]
You wouldn't think that stepping up just one
dimension from
circles in a plane to
spheres in a
volume would cause much more of a problem.
Greengrocers have been stacking fruit in nicely structured dense piles for centuries. However, proving that this arrangement, beloved by
Nature and
crystallographers as
face-centered-cubic (FCC), is indeed optimal, or that there is a non-lattice packing that's more dense, is quite a problem. None other than
Johannes Kepler first
conjectured that this FCC lattice, also called cubic close-packing, was the optimal packing of spheres. Calculation shows that the packing is (π/√18) = 0.74048, which means that there's quite a lot of empty space between spheres, a fact that allows the creation of the interesting material, inverse
opal.
Thomas Hales produced a "proof" of this conjecture in 1998. His proof, which is much like the "proof" for the
four color conjecture, used computer programs to examine every possible case of sphere packing. Checking such a proof is difficult, and even today
mathematicians are not completely certain that the proof is correct.[3] Even then, it would not be a proof in the usual sense of the word.
I've commented in several earlier articles that many scientific discoveries have been
accidental. One packing discovery happened accidentally at
Princeton University when a student was asked to experimentally measure random packing of a geometrical object. This object was
M&M candy, which is an
oblate spheroid. Surprisingly, a random assemblage of these was found to pack more densely than spheres, 68% as compared to 64% for random sphere packing.[4-6] The result was so surprising that
Paul Chaikin, a professor of
physics, repeated the experiment himself. He obtained the same result, and that led to a more detailed study. Other experiments showed that there was not much difference between spheres and M&Ms for lattice packing, only random packing.
Computer simulations showed that a random stacking of ellipsoids, which are closer in shape to a sphere than the lenticular M&M, yields a greater density than a lattice stacking of spheres.
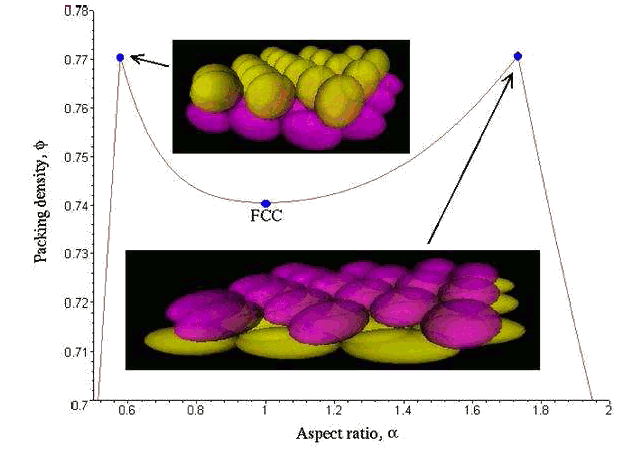
Density of the laminate crystal packing of ellipsoids as a function of the aspect ratio, via arXiv, Ref. 6.
What might be happening in such random packing is the idea that the elongated particles are able to slide past each other to a better equilibrium position, while the spheres jam together. Of course, experiments are tedious, and computer simulations are easier. It was found that there are a greater number of contact points between neighboring particles for the higher packing densities. The number of contact points may depend on the number of directions a particle can move and pivot.
Paul Chaikin has moved to
New York University, but
Salvatore Torquato, a professor of chemistry and co-investigator on the original M&M project, is still at Princeton publishing numerous papers in this area.[7-12] He was an author of a Physical Review Letter on packing in 2000, so he's been active in this area for more than a decade.[13] One interesting result is for the packing of the
Platonic solids. A
cube, of course, fills all space, but the densest packings of
tetrahedra,
icosahedra,
dodecahedra, and
octahedra were found to be 0.823, 0.836, 0.904, and 0.947. This is an interesting result, since the dodecahedra and icosahedra approximate a sphere to a high degree but pack much better.

Paul Chaikin (left) and Salvatore Torquato (Princeton University)
During the original research project about a decade ago,
Mars Inc., the M&M company, donated 125 pounds of almond M&M's; but men do not live by candy alone. Other funding came from the
National Science Foundation, the
NASA and the Petroleum Research Fund.
![]()
References:
- Weisstein, Eric W. "Circle Packing." From MathWorld--A Wolfram Web Resource.
- Tom Kennedy, "Compact packings of the plane with two sizes of discs," arXiv Preprint, July 8, 2004.
- Sphere Packing Page on Wikipedia.
- Steven Schultz, "Sweet science: Common candies yield physics discovery," Princeton University Press Release, February 12, 2004.
- Aleksandar Donev, Ibrahim Cisse, David Sachs, Evan A. Variano, Frank H. Stillinger, Robert Connelly, Salvatore Torquato and P. M. Chaikin, "Improving the Density of Jammed Disordered Packings Using Ellipsoids," Science, vol. 303, no. 5660 (February 13, 2004), pp. 990-993.
- Aleksandar Donev, Frank H. Stillinger, P. M. Chaikin and Salvatore Torquato, "Superdense Crystal Packings of Ellipsoids," arXiv Preprint, March 10, 2004.
- S. Torquato, "Reformulation of the Covering and Quantizer Problems as Ground States of Interacting Particles," arXiv Preprint, September 8, 2010.
- Salvatore Torquato and Frank H. Stillinger, "Jammed Hard-Particle Packings: From Kepler to Bernal and Beyond," arXiv Preprint, August 17, 2010.
- S. Torquato and Y. Jiao, "Exact Constructions of a Family of Dense Periodic Packings of Tetrahedra," arXiv Preprint, April 30, 2010.
- Y. Jiao, F. H. Stillinger and S. Torquato, "Novel Features Arising in the Maximally Random Jammed Packings of Superballs," arXiv Preprint, January 4, 2010.
- S. Torquato and Y. Jiao, "Dense Packings of Polyhedra: Platonic and Archimedean Solids," arXiv Preprint, September 9, 2009.
- S. Torquato and Y. Jiao, "Dense Packings of the Platonic and Archimedean Solids," arXiv Preprint, August 27, 2009.
- S. Torquato, T. M. Truskett and P. G. Debenedetti, "Is Random Close Packing of Spheres Well Defined?," Physical Review Letters, vol. 84, p. 2064 (2000).
Permanent Link to this article
Linked Keywords: penny; plane; synthetic a priori; hexagonal lattice; Carl Friedrich Gauss; László Fejes Tóth; root of a function; dimension; circle; sphere; volume; greengrocer; Nature; crystallography; crystallographers; face-centered-cubic; Johannes Kepler; Kepler conjecture; opal; Thomas Hales; four color conjecture; mathematician; serendipity; Princeton University; M&M candy; oblate spheroid; Paul Chaikin; physics; Computer simulation; New York University; Salvatore Torquato; Platonic solids; cube; tetrahedron; icosahedron; dodecahedron; octahedron; Mars Inc.; National Science Foundation; NASA; MathWorld; arXiv.