Martin Gardner
May 31, 2010
Word buffs have always had crossword puzzles, but the only recreation known to mathematicians until the mid-twentieth century was finding novel geometrical proofs for the
Pythagorean theorem, one of which is credited to US President
James A. Garfield. The construction of his proof is shown in the figure, from which the obvious solution can be derived (at least by my high school geometry teacher!). If you want to cheat, the solution can be found
here.
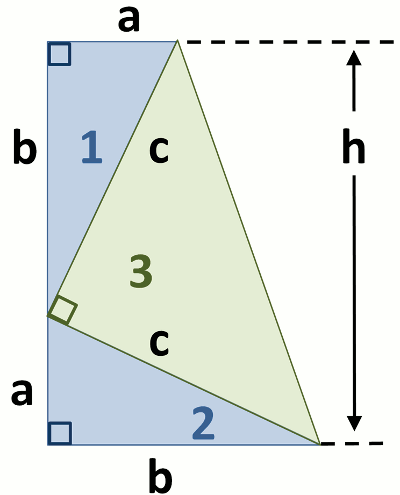
(Image by Brews ohare).
Of course, such proofs become more difficult as time goes on and all the obvious ones have been found. There are at least 370 [1]. A revival in recreational mathematics occurred in 1956 with inception of the Mathematical Games column in Scientific American. This column, which appeared from 1956-1981 was written by Martin Gardner, a veteran science writer who died May 22, 2010, at age 95 [2].
The amazing thing was that Gardner, who was venerated by the mathematician and fellow author,
Rudy Rucker, and the physicist and fellow author,
Douglas Hofstadter, never took a mathematics course beyond high school. Said Gardner, "There is no better way to learn anything than to write about it!" [2]
One thing that I had in common with Gardner was the idea that mathematics is discovered, not invented. I wrote about this philosophical debate in a
previous article (Mathematical Objects, May 09, 2008). This way of looking at mathematics is called the
Platonist view, and we can count among our fellow Platonists the prominent mathematician,
Roger Penrose. One argument that favors discovery is the existence of the constant, pi, the ratio of the circumference to the diameter of a circle. The number, pi, is part of many fundamental equations of physics, which indicates to me that pi has a physical reality independent of an observer.
Gardner's best legacy was legitimizing computers as an important part of mathematics. The proof of the
four-color conjecture, a proof done completely by computer, was uniformly derided by professional mathematicians as not being a
real proof. Gardner, however, wasn't a professional mathematician, so he wasn't bothered by any concept of mathematical purity. One of his most popular articles was about
John Conway's Game of Life, a computer excursion into
cellular automata. This computer simulation, known to all computer literate people, involves the evolution of a population on a checkerboard array. The individuals of this population are black spots who live alone in separate cells on the white board and obey these simple rules:
- Any person with fewer than two neighbors dies (underpopulation).
- Any person with more than three neighbors dies (overcrowding).
- Any person with two or three neighbors lives on to the next generation (subsistence).
- Any empty cell with exactly three live neighbors generates a new person (birth).
The board is initially populated and the computer cranks through the generations by applying these rules simultaneously to each cell on the board, over and over again. Some populations become extinct very quickly, while others give unusual patterns of motion across the board.
Conway's Game of Life simulation introduced cellular automata to mathematics, but the rapid growth of this branch of mathematics is the result of Gardner's article. A notable practitioner of computer automata is
Stephen Wolfram, who made somewhat of a religion out of them in his book, "
A New Kind of Science." Wolfram is famous not only for this book, but for creating the symbolic computation program,
Mathematica; and for resigning from the physics faculty of the
California Institute of Technology over intellectual property rights to a computer algebra system, called SMP [3]. Wolfram is now the millionaire owner of
Wolfram Research, and I bet that CalTech isn't expecting a donation of a Wolfram Computer Center anytime in the future.
References:
- Elisha Scott Loomis, "The Pythagorean proposition: its demonstrations analyzed and classified, and bibliography of sources for data of the four kinds of proofs," Education Resources Information Center. Institute of Education Sciences (IES) of the U.S. Department of Education (1940); reprinted in 1968 by National Council of Teachers of Mathematics (PDF File).
- Emma Brown, "Martin Gardner," Washington Post Online(May 23, 2010).
- Gina Kolata, "Caltech Torn by Dispute Over Software," Science, vol. 220, no. 4600 (May 27, 1983)pp. 932-934.
- Philip Yam, "Profile: Martin Gardner, the Mathematical Gamester (1914-2010)," Scientific American Online (May 22, 2010).
- Game of Life
- Interview with Martin Gardner, Notices of the AMS, vol. 52, no. 6 (June/July, 2005), pp. 602-611.
- Wikipedia article on Martin Gardner.
Permanent Link to this article