Big G
October 12, 2010
There are two constants associated with gravity - "Big G" and "little g." The constant associated with the
gravitational acceleration of objects to
Earth,
g, is not really a constant, since it varies slightly from place to place on the surface of the Earth. The textbook value of
g is 9.80665 m/s
2. The other
gravitational constant,
G, is the constant of the
Newtonian gravitational force equation,
F = G m1 m2/r2.
The
CODATA value of
G is 6.67428 x 10
-11 m
3 kg
-1 s
-2, or 6.67428 x 10
-11 N (m/kg)
2. The value of
g depends, of course, on the value of
G. We just plug Earth's
mass and
radius into the force equation and note that the mass of the Earth is much larger than that of our test mass. As text books are wont to say, the calculation is left to the reader.
Many physical constants are known to very high precision, since they are the bellweathers of the validity of many physical theories. For example, the
fine structure constant is known to eleven significant figures. In contrast to this, the relative standard uncertainty of
G is 1 part in 10
4. As I summarized in a
previous article (Gravitation, January 25, 2007), it's not that physicists haven't been trying to get a better value. It's because the
force of gravity is very small. For example, the repulsive electrical force between two electrons is nearly 10
43 times stronger than their gravitational attraction.
The first measurement of
G was made in the period 1797-1798 by the British physicist,
Henry Cavendish. Cavendish used equipment designed by a geologist, John Michell, and his purpose was to measure the density of the Earth. The apparatus, however, served both purposes. Michell had died in 1793, and his apparatus was sent to Cavendish, who made improvements to lessen the affects of temperature and air currents.[1]
The apparatus, as shown in schematic form in the figure, was a
torsion balance that measured the force of gravity between a pair of 1.61 pound lead spheres and two 350 pound lead spheres. Since gravitational attraction between such small masses is very small, the twisting force on the torsion wire was only a little more than 10
-7 Newton. In order to make sense of the torsion measurements, you need to know the
spring constant of the torsion fiber. This is done by measuring the
resonant frequency of the torsion balance. All such problems notwithstanding, Cavendish obtained values that correspond to a
G accurate to about 1%. Cavendish, however was not interested in
G, so his paper on
his experiment, published in 1798 in the
Philosophical Transactions of the Royal Society, gave only his value for Earth's density, about 5.48. I did the Cavendish experiment in an undergraduate physics laboratory in 1966. As I remember, our lead balls were somewhat smaller. There was the practical problem of stowing the apparatus when it wasn't in use, and two 350 pound lead spheres would have made this difficult.
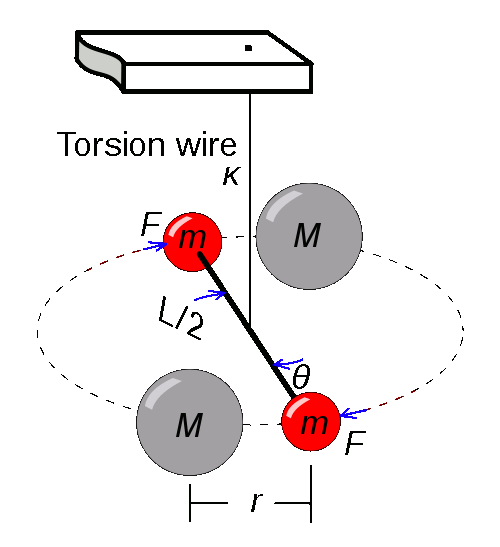
(diagram by Chris Burks).
As it turned out, the torsion balance method of measurement, with improvements, was the best method of measuring
G. The last such measurement, by Jens Gundlach and Stephen Merkowitz in 2000 at the
University of Washington (
Seattle) gave a value of 6.674215 x 10
-11 m
3 kg
-1 s
-2, with a claimed uncertainty of 14 ppm.[2]
In August, this value of
G was called into question by a measurement that uses a different technique. It's always good to use new technologies to improve measurements, and this is what Harold Parks and James Faller of
Sandia National Laboratory (
Albuquerque, New Mexico) did. They used laser interferometry to make precise measurements of the way the motion of pendulums are affected by nearby masses.[2,3] Their apparatus can be seen in the figure.
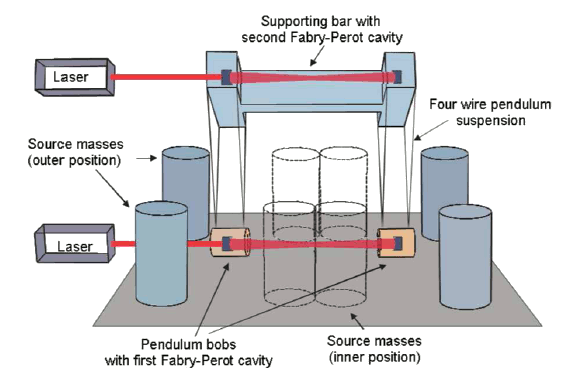
The Parks and Faller experiment (via arXiv, Ref. 3).
Laser interferometry is a very sensitive way to measure deflection. In this case there are complementary pendulum bobs that combine to form
Fabry-Perot resonators. There's a simultaneous measurement of the position of the pivot points of the pendulums to remove any affects of temperature. All in all, this is a very nicely designed experiment.
Parks and Faller were likely expecting a value for
G very close to the University of Washington value. Instead, they measured 6.67234 x 10
-11 m
3 kg
-1 s
-2, with a claimed uncertainty of 21 ppm. This is ten
standard deviations below the University of Washington value.[2] Whose value is right? The University of Washington value is consistent with previous experiments, but these were all Cavendish-style torsion pendulum experiments. Parks and Faller have listed all error sources in their measurement, as shown in the table.
| Uncertainty Component | δG/G (x10-5) |
| Six critical dimensions | 1.4 |
| All other dimensions | 0.8 |
| Source mass density inhomogeneities | 0.8 |
| Pendulum spring constants | 0.7 |
| Total mass measurement | 0.6 |
| Interferometer | 0.6 |
| Tilt due to source mass motion | 0.1 |
| Day-to-day scatter | 0.4 |
| Combined uncertainty | 2.1 |
I'm not a metrology expert, but as a materials scientist I'm immediately attracted to possible problems with the spring constant measurement of torsion pendulums. Things might not be fully
elastic, and non-linear effects are possible. It might be time to start work on a carbon nanotube torsion pendulum.
References:
- An excellent summary of the Cavendish Experiment on Wikipedia.
- Eugenie Samuel Reich, "G-whizzes disagree over gravity," Nature, vol. 466, no. 7310 (August 26, 2010), p.1030.
- Harold V. Parks, James E. Faller, "A Simple Pendulum Determination of the Gravitational Constant," arXiv Preprint (September 7, 2010); PDF version of the paper is available here.
Permanent Link to this article
Linked Keywords: Gravitational acceleration; Earth; gravitational constant; Newtonian gravitational force; CODATA; Earth mass; Earth radius; fine structure constant; force of gravity; Henry Cavendish; torsion balance; spring constant; resonant frequency; Cavendish experiment; Philosophical Transactions of the Royal Society; University of Washington; Seattle; Sandia National Laboratory; Albuquerque, New Mexico; Parks and Faller experiment; Fabry-Perot; standard deviations; elastic.