Aperiodic Tiling
August 14, 2023
Apparently,
women seem to notice
shoes; and, in some cases this
excitement about shoes goes to excess. Former
First Lady of the Philippines,
Imelda Marcos (b. 1929), is
reported to have had more than a thousand pairs of shoes. I, however, never notice shoes and seldom look down. I did look down recently when my
wife was on her
knees,
scrubbing the
kitchen floor,[1] and I noticed again that the floor
tiles there are a simple
array of
squares.
Variations of floor tiling
patterns have existed from
antiquity, as
archaeology of
Pompeii illustrate.
Tessellation is the formal term for a
two dimensional tiling.
Tiling with regular polygons, such as that of my kitchen floor, is easily achieved with squares,
equilateral triangles and
hexagons. Of course, hexagons are made from equilateral triangles; so, there's no
surprise there.

An ancient Roman geometric mosaic, now sited at the Palazzo Massimo alle Terme, National Roman Museum of Rome, Italy. This rhombic tiling has a stacked cube optical illusion. Wikimedia Commons image by "Mbellaccini."
Johannes Kepler (1571-1630), in Book II (On the Congruence of Regular Figures) of his 1619
Harmonices Mundi,
published the first detailed study of
regular polygons tilings.[2-3] In that book, Kepler
cataloged eleven uniform tilings of the
plane (see example).[2-3] He showed, also, that you can't fill a plane with
regular pentagons. Tiling on a plane with regular pentagons is not possible because the
internal angle of a regular pentagon, 108°, is not a
divisor of 360°. Tiling is possible with
irregular pentagons.
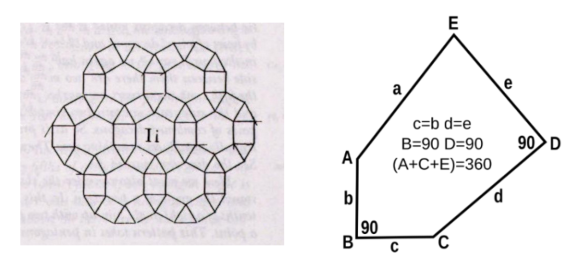
Image from Book II of Harmonices Mundi (left) and an irregular pentagon suitable for tiling (right). There are fifteen irregular pentagons known to tile the plane as the only tile needed, and it's conjectured that these fifteen are the only ones possible. (Left image from Book II of Harmonices Mundi, via Google Books. Right image created using Inkscape.)
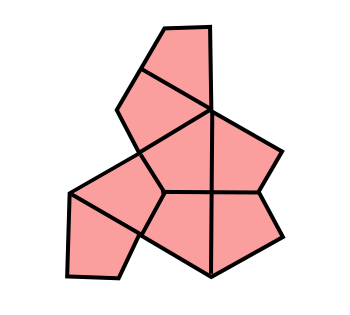
There is more variation when more than one type of polygon is allowed for the tiling. While the five-fold
rotational symmetry of a regular pentagon alone will not tile a plane, a combination of two polygons, as shown in the figure, will produce a tiling with
five-fold symmetry.

A tiling with five-fold rotational symmetry based on two rhombi.
This is a Penrose tiling, named after the mathematical physicist, Roger Penrose (b. 1931).
Penrose was issued a patent on his tiling in 1979.[4]
(Modified Wikimedia Commons image. Click for larger image.)
A 13-sided tile that
aperiodically fills a plane has been discovered by an
eclectic group of
mathematicians and
computer scientists.[5-8] The
authors are David Smith, a self-described
shape hobbyist of
East Yorkshire, England, Joseph Samuel Myers, a
software developer of
Cambridge, England,
Craig S. Kaplan of the
University of Waterloo (Waterloo, Ontario, Canada), and
Chaim Goodman-Strauss of the
University of Arkansas (Fayetteville, Arkansas). This object, called an
einstein, is built from eight
kite shapes. This aperiodic monotile is not named for
German physicist,
Albert Einstein (1879-1955), but from the
German phrase for
one stone.[6]
The thirteen-sided monotile for aperiodic tiling, an "einstein," is composed of eight "kite" sections.
(Created using Inkscape from data in ref. 5.)[5]
Mathematicians had long searched for aperiodic tilings, and one first success used a set of 20,426 tiles.[6-7] After Penrose pared the number to two tiles, there's been a search for a monotile that would accomplish the task, but it wasn't apparent that such a tiling could exist.[6,8] David Smith, who is a retired
printing technician as well as a
nonprofessional mathematician, found such a monotile, mostly by
intuition and
experimentation.[8]
Smith would
cut promising shapes from
card stock to see how they fit together.[7] The basis unit of the monotile is the kite shape, shown in the figure, and these kites were combined to become the polykite monotile that the authors call the
hat.[5] As Smith told the
Guardian, "I am quite persistent but I suppose I did have a bit of
luck."[7] He enlisted the aid of his coauthors to mathematically prove his conjecture.[8] The shape is simpler than expected.[8] One
proof, created by Myers led to another monotile that the authors call the
turtle.[7]
It appears that the only applications for this tiling are
decorative.[6] As Kaplan told the Guardian, "There are lots of great real-world applications in
art,
design,
architecture... The race is on to be the first person to take a
photo of their
bathroom floor tiled in hats."[7]

An aperiodic tiling of 13-sided monotiles. The white tiles are flipped with respect to the others, and these are always surrounded by a set of three unflipped tiles, shown in blue. (Created using Inkscape from data in ref. 5.[5] Click for larger image.)
References:
- No, she wasn't also barefoot and pregnant, and I did offer some assistance.
- Johannes Kepler, "The Harmony of the World," English translation of Harmonices Mundi (1619) by the American Philosophical Society, 1997, via Google Books.
- Kevin Jardine, "Kepler and the regular polygon tilings," http://gruze.org. This website includes many images in its Tiling Gallery.
- Roger Penrose, "Set of tiles for covering a surface," US Patent No. 4,133,152, January 9, 1979 (via Google Patents).
- David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss, "An aperiodic monotile," arXiv, March 20, 2023, https://doi.org/10.48550/arXiv.2303.10798.
- Bob Yirka, "A geometric shape that does not repeat itself when tiled," phys.org, March 23, 2023.
- Matthew Cantor, "The miracle that disrupts order: mathematicians invent new 'Einstein' shape," Guardian (UK), April 4, 2023.
- Will Sullivan, "At Long Last, Mathematicians Have Found a Shape With a Pattern That Never Repeats," Smithsonian Magazine, March 29, 2023.
Linked Keywords: Woman; women; shoe; pleasure; excitement; First Lady of the Philippines; Imelda Marcos (b. 1929); report; wife; knees; scrubbing; kitchen; floor; tile; array; square; pattern; antiquity; archaeology; Pompeii; tessellation; two-dimensional space; Euclidean tilings by convex regular polygons; tiling with regular polygons; equilateral triangle; hexagons; surprise (emotion); ancient Roman; geometry; geometric; mosaic; Palazzo Massimo alle Terme, National Roman Museum of Rome, Italy; rhombus; rhombic; tiling; stack; cube; optical illusion; Wikimedia Commons; Johannes Kepler (1571-1630); Harmonices Mundi; publication; publish; cataloging (library science); cataloged; plane (geometry); regular pentagon; internal angle; internal angle; divisor; pentagon tiling; irregular pentagon; conjecture; Google Books; Inkscape; rotational symmetry; symmetry; five-fold symmetry; Penrose tiling; mathematical physics; mathematical physicist; Roger Penrose (b. 1931); patent; aperiodic tiling; aperiodically; eclectic; mathematician; computer scientist; authors; geometry; shape; hobby; hobbyist; East Yorkshire, England; software developer; Cambridge, England; Craig S. Kaplan; University of Waterloo (Waterloo, Ontario, Canada); Chaim Goodman-Strauss; University of Arkansas (Fayetteville, Arkansas); kite; Germany; German; physicist; Albert Einstein (1879-1955); German language; phrase; rock (geology); stone; monotile; kite; Inkscape; printing; technician; professional; nonprofessional; intuition; experiment; experimentation; cut; card stock; hat; The Guardian; luck; mathematical proof; turtle; decorative arts; art; design; architecture; photograph; bathroom; reflection (mathematics); flipped; barefoot and pregnant; Roger Penrose, "Set of tiles for covering a surface," US Patent No. 4,133,152, January 9, 1979.