Disjunction
February 15, 2021
Some
religions see
enlightenment in contemplation of the
navel, but
mathematicians have been
fascinated by something of
analogous shape, the
number zero (0). The
ancient Greeks had a problem with the
concept of zero (μηδέν, minden), and they had no
symbol for it. Their
argument was, "How can nothing be something?" They had similar problems with the idea of a
vacuum. The
paradoxes of
Zeno of Elea (c.495-c.430 BC) arose from the idea that a zero quantity was unattainable (see figure).
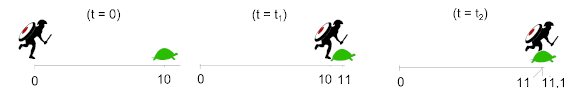
In Zeno's Paradox of Achilles and the Tortoise, Achilles can never outrun a tortoise having a head start, since he must always reach the point where the tortoise once was, but departed, with the consequence that the tortoise can never be overtaken. This paradox expresses the idea that the distance between Achilles and the tortoise can never be zero; and, therefore, zero can't be transcended to change the sign of that distance. This was my favorite paradox when I was a high school student. (Modified Wikimedia Commons image by Daniele Pugliesi. Click for larger image.)
Moving ahead into
Anno Domini times,
Ptolemy (c.100-c.170) was using a symbol for zero, a small
circle with a
line above it, around 150 AD in his
Almagest. Zero in
Latin texts throughout the
Middle Ages was much different, being essentially the
letter,
N, used as
shorthand for
nulla (none) or
nihil (nothing). By the start of the
18th century, the use of our present symbol for zero was firmly entrenched in Latin. It was used by
Leonhard Euler (1707-1783), who wrote many
mathematics papers in Latin, as the following example illustrates.

Proposition 4 from De summatione innumerabilium progressionum (1738) by Leonhard Euler, illustrating the use of the symbol for zero. In translation it reads, "§4. This form is assumed as the general term of a certain progression: ∫((1-xn)/(1-x))dx; which clearly integrated, thus so that it becomes equal to zero if x = 0, and on putting x = 1, the term of order n is given." Latin text from Ref. 1, and English translation from Ref. 2.[1-2]
All people are familiar with the basic mathematical symbols for
addition (+),
subtraction (−),
multiplication (×),
division (÷), and the
square root (√), and most
technologists know also the symbols for
summation (∑) and
integration (∫), as well as those for
comparison; i.e., less than (<), greater than (>), less than or equal (≤), and greater than or equal (≥). Lesser known are the basic symbols of
symbolic logic. Two of these are
contortions of
Roman alphabet letters; namely, the
existential quantification operator (∃, normally expressed as "there exists," as in ∃(x), "there exists an x"), and the
universal quantification operator (∀, "for all." as in ∀(x), "for all x").
Other symbols in mathematical logic are the symbols for "and" (⋀), "or" (⋁), and also
material conditional (⊃, also written as →) that's used in statements such as
modus ponens; viz,
If P, then Q (P⊃Q)
P is true
Therefore, Q is true.
You can view many
unicode characters in the category, "Math Symbol," at Ref. 3.[3]
Landon D. C. Elkind of the
University of Alberta (Edmonton, Alberta, Canada), and
Richard Zach of the
University of Calgary (Calgary, Alberta, Canada) have recently
published a lengthy
paper on
arXiv in which they've investigated the origin of the symbol for
logical disjunction ("or," ⋁).[4] It has been suggested by many
historians that, just as
N was chosen to represent zero from the first letter of the Latin words that express nothingness, ⋁ merely derives from the first letter of the Latin word for
or; namely,
vel.[4]
Leibniz had used the letter
v with an
accent mark called the
inverted breve, ͡v, as the disjunction symbol.
Peano remarked that this symbol without the accent is a sensible choice because
v is the initial letter of
vel.[4]
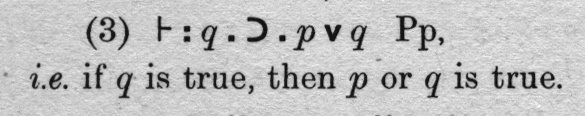
Excerpt from Principia Mathematica by Alfred North Whitehead (1861-1947) and Bertrand Russell (1872-1970) showing use of the disjunction symbol. (Portion of a scan of page 13 of my copy.[5])
While Peano made a case for using a
v for disjunction, he didn't follow his own advice. Instead, he used the
union symbol, ∪, from
set theory.[4] Elkind and Zach conclude that Bertrand Russell's use of the symbol is what codified its place in
symbolic logic.[4] Russell tended to follow Peano's lead in
notation, and Whitehead and Russell's Principia Mathematica was influential in mathematical logic.[4] As Elkind and Zach write,
"The appealing short story told that our '∨' for disjunction comes from the Latin vel and is due to Leibniz is not well-supported by the textual record. It was Russell, not Leibniz, who first systematically used ‘∨’ for disjunction, and it is more likely given Russell’s logical habits that this choice of notation was to stress the analogy of propositional addition with class union."[4]
References:
- Leonhard Euler, "De summatione innumerabilium progressionum," Commentarii academiae scientiarum Petropolitanae, vol. 5 (1730/31), published 1738, pp. 91-105, from the Euler Archive.
- Leonhard Euler, "De summatione innumerabilium progressionum (Concerning the Summation of Innumerable Progressions)," Commentarii academiae scientiarum Petropolitanae, vol. 5 (1730/31), published 1738, pp. 91-105, Translated and annotated by Ian Bruce.
- List of Unicode Characters of Category "Math Symbol," Compart AG Website.
- Landon D. C. Elkind, and Richard Zach, "The Genealogy of ⋁, arXiv, December 14, 2020.
- Alfred North Whitehead and Bertrand Russell, Principia Mathematica to *56, Cambridge University Press, Reprint edition, January 1, 1964, 410pp.
Linked Keywords: Religion; navel gazing; enlightenment; contemplation; navel; mathematician; fascination; fascinated; analogy; analogous; shape (geometry); number zero (0); ancient Greece; ancient Greeks; concept; symbol; argument; vacuum; Zeno's paradoxes; Zeno of Elea (c.495-c.430 BC); Zeno's Paradox of Achilles and the Tortoise; Achilles; tortoise; paradox; sign (mathematics); high school student; Wikimedia Commons; Daniele Pugliesi; Anno Domini; Ptolemy (c.100-c.170; circle; line segment; line; Almagest; Latin; Middle Ages; letter (alphabet); shorthand; 18th century; Leonhard Euler (1707-1783); mathematics; theorem terminology; proposition; translation; geometric progression; integral; integrated; addition; subtraction; multiplication; division (mathematics); square root; technology; technologist; summation; inequality (mathematics); comparison; first-order logic; symbolic logic; contortion; Latin alphabet; Roman alphabet; existential quantification; universal quantification; material conditional; modus ponens; unicode character; Landon D. C. Elkind; University of Alberta (Edmonton, Alberta, Canada; Richard Zach; University of Calgary (Calgary, Alberta, Canada); academic publishing; published; scientific literature; paper; arXiv; logical disjunction; historian; Gottfried Leibniz; diacritic; accent mark; inverted breve; Giuseppe Peano; Principia Mathematica; Alfred North Whitehead (1861-1947); Bertrand Russell (1872-1970); union (set theory); set theory; mathematical logic - symbolic logic; notation; short story; habit; propositional formula; propositional addition.