Bottle Flow
June 15, 2020
As they say, "
A place for everything, and everything in its place," which is a
proverb attributed to
Benjamin Franklin (1706-1790). In
households, this place is usually a
jar or
bottle for containing a
liquid. Some liquids are
watery, so they
flow easily out of their container. However, others like
ketchup are
thick, so they present a
fluid flow problem. While my preferred ketchup bottle is the newer,
plastic squeeze bottle that performs ketchup extraction perfectly, ketchup was only available in
glass bottles until recently.
The common technique for getting ketchup to flow from a glass bottle is to
hit the bottle with the
palm of your
hand. Ketchup is a
non-Newtonian fluid, and such fluids will change
viscosity with application of external
forces. Other examples of non-Newtonian flow are the
blood coursing through your
arteries and
veins, and
inkjet printing.
Rheology, from the
Greek words, ρεω (rheo,
flow) and λογια (logia,
the study of), is a branch of
mechanics for the study of flow. The
motto of
The Society of Rheology is πάντα ῥεῖ (panta rei,
Everything Flows). This expression is associated with the
5th century BC, the
Greek philosopher,
Heraclitus of Ephesus, who also observed that
you can't step in the same river twice, since it would have changed in between steps. Heraclitus considered
fire to be the most fundamental
element and progenitor of all the other
elements.

Logo of The Society of Rheology.
The Society of Rheology was officially formed on December 19, 1929, and it was one of the five founding members of the American Institute of Physics.
The Society of Rheology has fewer than 2,000 members, and it publishes the Journal of Rheology.
(Society of Rheology image.)
The
Roman philosopher,
Lucretius (c. 99 BC - c. 55 BC), wrote about rheology in his
book,
De Rerum Natura (On the Nature of Things), Book II, ll. 391-397.[2-3]
"We see how quickly through a colander the wines will flow; how, on the other hand, the sluggish olive oil delays: no doubt, because 'tis wrought of elements more large, or else more crook'd and intertangled. Thus it comes that the primordials cannot be so suddenly sundered one from other, and seep, one through each several hole of anything."[3]
Lucretius proposes using a
colander as a
rheometer. Many of today's
laboratory rheometers function by the same principle by measuring the time it takes for fluid to flow through a
pipe or
capillary. Other rheometers examine the
force transmitted through the fluid from a moving
surface to another surface.
Isaac Newton (1642-1727), proposed a
theory of
viscosity, the resistance to flow, in his
Principia, where he writes, [4-5]
"The resistance which arises from the lack of slipperiness of the parts of the liquid, other things being equal, is proportional to the velocity with which the parts of the liquid are separated from one another."
Viscosity is the
scientific term for Newton's "lack of slipperiness."
Small flow
channels have a different viscosity law.
Physicists at the
Georgia Institute of Technology used
atomic force microscopy (AFM) to find that confinement of a low viscosity fluid in a
nanometer-scale channel causes the fluid to become more viscous.[6] Their
experiments showed that the
viscoelastic relaxation times for
water and
silicone oil confined in such nanometer-sized channels are
orders of magnitude longer than the usual values.[6] The relaxation times for water were as slow as a tenth of a
second at
room temperature, which is comparable to that for
supercooled water at 170-210
kelvin.[6] The ketchup effect was still present, since shaking reduced this scale-induced viscosity.[6]
While viscosity of the liquid is a huge factor affecting the emptying of a bottle, another factor is the necessity of
air getting back through the opening, forming a
bubble that replaces the missing liquid. Bubbles are fascinating to
children, and they also fascinated
Leonardo da Vinci (1452-1519), who wrote about the motion of air bubbles in water in the
Codex Leicester, the main topic of which is
fluid dynamics.[8]
The bubble
dynamics of bottle emptying was recently investigated by two
mechanical engineers at the
Indian Institute of Technology (Roorkee, India) and
published in a recent issue of the
journal,
Physics of Fluids.[7-8] They used
high-speed photography to examine the bubble dynamics for a
commercial bottle containing water,
glycerol, and silicone oil.[8] Their
research of the
rate at which bottles empty has applications beyond the
food industry.[8]
TABLE. Properties of the studied fluids at 30 °C.
Says study
author,
Lokesh Rohilla, "Bubble dynamics inside the bottle are too complex to study, so we divided the bubble
interfacial growth into different stages to comprehend them."[8] A
phenomenon that everyone has experienced is that bottles will empty faster when they're
angled from the
horizontal. This increases what's called the bubble pinch off
frequency, and this angle depends on the fluid properties.[8] If the bottle opening is too small,
surface tension forces prevent the fluid from exiting. If the bottle opening is larger, a
spherical bubble train with a
rhythmic pinch-off frequency forms. Bottle opening of larger size allows creation of a channel of air entering the liquid. When the
diameter increases to the point at which the bottle is a
cylinder, the liquid moves out as a
rigid body.[7]
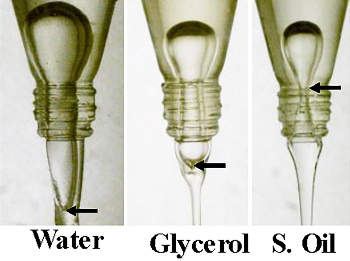
Formation of encapsulated bubbles in water, glycerol, and silicone oil, showing where bubble pinch-off occurs.
Says study author, Lokesh Rohilla, "We've also observed an encapsulated bubble while discharging fluid in a vertically upended bottle... Encapsulated bubbles have pinch off sites outside the bottle mouth, contrary to intuition."[8]
(American Institute of Physics image by Lokesh Rohilla.)
Everyone wants their ketchup faster, and the researchers founds that the bottle emptying time was reduced by decreasing the
volume of each pinched-off bubble and increasing pinch-off frequency for low viscosity liquids, such as water; or, by increasing the volume of each pinched-off bubble at a comparatively lower frequency for high viscosity liquids such as glycerol and silicon oil.[7] No matter the liquid, an
asymptotic emptying point was found at a change in mode from slugging to a
stratified pattern.[7] This happened in all liquids at about 20
degrees inclination for the particular bottle used (see figure).[7]
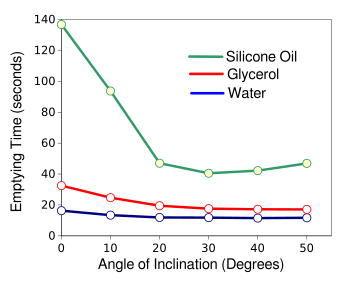
The effect of the angle of inclination on emptying time for the three different fluids.
In each case, the asymptote appears at about 20 degrees of inclination for the particular bottle used in the experiments.
(Created using Gnumeric from data in Table II of ref. 7.[7])
The principal finding of the study is the asymptote that occurs at a particular angle, irrespective of the fluid properties.[7] Says Rohilla,
"Our experiments suggest there is a critical angle of inclination, after which any further increase in the inclination of the bottle won't lead to further reduction in the bottle emptying time... This occurs due to the saturation of the voidage, space occupied by air within liquid surrounding, at the bottle's mouth with the angle of inclination."[8]
As
corresponding author,
Arup Kumar Das, states, "We can manipulate the bottle discharge pattern by manipulating bottle
geometry... An intuitive product-specific bottle design will enable better control of its discharge rate."[8]
References:
- About The Society of Rheology, The Society of Rheology Website.
- TITI LVCRETI CARI DE RERVM NATVRA LIBER SECVNDVS, Book II, ll. 391-397, Latin Text, via The Latin Library.com.
"Et quamvis subito per colum vina videmus
perfluere, at contra tardum cunctatur olivom,
aut quia ni mirum maioribus est elementis
aut magis hamatis inter se perque plicatis,
atque ideo fit uti non tam diducta repente
inter se possint primordia singula quaeque
singula per cuiusque foramina permanare."
- Lucretius, "On the Nature of Things," Translated by William Ellery Leonard, Book II, ll. 391-397, via Classics.MIT.edu.
- Roger I. Tanner and Kenneth Walters, "Rheology: an historical perspective," Elsevier, 1998, 255 pages.
- I.S. Newton, "Philosophiae Naturalis Principia Mathematica," 1st Ed., 1687, Bk 2, Sect. IX, via Project Gutenberg. In Latin,
"Resistentiam, quae oritur ex defectu lubricitatis partium Fluidi, caeteris paribus, proportionalem esse velocitati, qua partes Fluidi separantur ab invicem."
- Tai-De Li and Elisa Riedo, "Nonlinear Viscoelastic Dynamics of Nanoconfined Wetting Liquids," Phys. Rev. Lett. vol. 100, no. 10 (March 14, 2008), p. 106102, DOI:https://doi.org/10.1103/PhysRevLett.100.106102.
- Lokesh Rohilla and Arup Kumar Das, "Fluidics in an emptying bottle during breaking and making of interacting interfaces," Physics of Fluids, vol. 32, no. 4 (April 7, 2020), Article no. 042102, https://doi.org/10.1063/5.0002249. A PDF file of this paper is presently available here.
- Bubble dynamics reveal how to empty bottles faster, American Institute of Physics Press Release, April 7, 2020.
Linked Keywords: A place for everything, and everything in its place; proverb; Benjamin Franklin (1706-1790); household; jar; bottle; liquid; watery; flow; ketchup; thick; fluid dynamics; fluid flow; plastic; squeeze bottle; glass; impact (mechanics); hit; hand area palm; hand; non-Newtonian fluid; viscosity; force; blood; circulatory system; course; artery; vein; inkjet printer; inkjet printing; rheology; Greek language; Greek word; classical mechanics; motto; The Society of Rheology; 5th century BC; Ancient Greek; philosopher; Heraclitus of Ephesus; you can't step in the same river twice; Fire (classical element); classical element; logo; American Institute of Physics; Journal of Rheology; Roman philosophy; Roman philosopher; Lucretius (c. 99 BC - c. 55 BC); book; De Rerum Natura; colander; wine; olive oil; rheometer; laboratory; pipe (fluid conveyance); capillary; surface; Isaac Newton (1642-1727); theory; Philosophiae Naturalis Principia Mathematica; Principia; proportionality (mathematics); proportional; velocity; science; scientific; microchannel (microtechnology); channel; physicist; Georgia Institute of Technology; atomic force microscopy (AFM); nanometer-scale channel; experiment; viscoelasticity; viscoelastic; relaxation time; order of magnitude; second; room temperature; supercooling; supercooled water; kelvin; atmosphere of Earth; air; bubble (physics); child; children; Leonardo da Vinci (1452-1519); mechanical engineering; mechanical engineer; Indian Institute of Technology (Roorkee, India); scientific literature; publish; scientific journal; Physics of Fluids; high-speed photography; commerce; commercial; glycerol; research; speed; rate; food industry; density; surface tension; inverse viscosity number; author; Lokesh Rohilla; interface (chemistry); interfacial; phenomenon; angle; angled; horizontal; frequency; sphere; spherical; rhythm; rhythmic; diameter; cylinder (geometry); rigid body; encapsulate; Lokesh Rohilla; vertical; restrictive flow orifice; mouth; intuition; volume; asymptote; asymptotic; stratification; stratified pattern; degree (angle); grade (slope); inclination (slope); Gnumeric; corresponding author; Arup Kumar Das; geometry.