Math is Beautiful
December 9, 2019
While
Cicero's orations have long since faded from my
memory, I fondly remember a few pertinent
Latin adages. One of these is "
De gustibus non disputandum est," which is often rendered in the not precisely
grammatical, "De gustibus non est disputandum." The
translation of this is "about taste there can be no argument," which means that "
one man's trash is another man's treasure."
Abstract art is enjoyed by many, although some think it can be
painted by a monkey. "
Beauty is in the eye of the beholder" is a similar adage.

I've always enjoyed the abstract expressionalist works of Mark Rothko (1903-1970). However, our present era of near-perpetual copyright prevents me from showing any of his work.
Instead, this is a photograph entitled, "Sun through the curtains II," by David Barrie that's in Rothko's style. There's a Flikr group with nearly a hundred thousand photos of this type.
(Wikimedia Commons image.)
One pleasing aspect of
art is its
symmetry, and the symmetry present in many objects of
science and
mathematics is also considered to be beautiful. I discussed symmetry and the concept of beauty in science in a
recent article (Is Science Simply Beautiful? August 26, 2019). In 2016, the
BBC did an
online poll to have the
public select the
most beautiful equation from a list of candidates proposed by
physicists and
mathematicians. The results, although not scientific, are still interesting; and, what is just as interesting, is that the equation for the
Pythagorean theorem didn't make the list. At the least, we have a list of the twelve selected
equations (see graph).
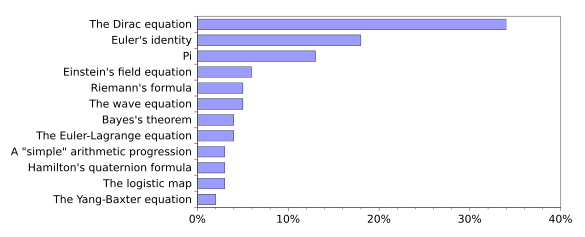
A beauty poll of twelve equations from physics and mathematics. Any physicist worth his salt should be familiar with at least ten on this list, but I must confess that I didn't know the Yang–Baxter equation until I checked Wikipedia. (Created using Gnumeric. Click for larger image.)
It appears that the online
voters knew their topic area, since the winner by far was the
Dirac equation. This equation, which describes
massive spin-1/2 elementary particles such as the
electron, is significant for two reasons. It was the result of the first
theory that combined
special relativity and
quantum mechanics, and it predicted
antimatter in the form of the
positron. The originator of this equation,
Paul Dirac (1902-1984), shared the 1933
Nobel Prize in Physics with
Erwin Schrödinger (1887-1961), who has another equation on this list, the
Schrödinger wave equation.
Although
Pythagoras (c.570-c.495 BC) didn't make the list,
Leonhard Euler (1707-1783) did, in the form of
Euler's Identity,
eiπ + 1 = 0
This equation combines five
fundamental mathematical constants, 0, 1,
e,
i, and
π, with the
fundamental mathematical operations of
addition,
multiplication, and
exponentiation. You obtain this equation by evaluating
Euler's formula,
eix = cos(x) + isin(x), at
x = π.
While we recognize that something like an equation can be considered beautiful, we shouldn't equate beauty and
truth.
Massimo Pigliucci, a
professor of
philosophy at the
City University of New York, has
criticized the
idea that truth can be recognized by beauty and
simplicity.[2] For example, one
motivation for
string theory is the idea that beauty demonstrates truth even when
experiment is not possible for
validation; that is, when
falsifiability is not possible.[2-4]
Mathematical beauty is less controversial, since many mathematicians see math as an
art form comparable to
composing music. There's also the fact that, unlike string theory,
mathematical proofs can be inexpensively validated; and, simplicity in a proof is beautiful when it makes this validation easier to perform and easier for a
student to see.
Number theorist,
G. H. Hardy (1877-1947), wrote in his 1940
book, "
A Mathematician's Apology," that he was happy that his mathematics (like art) was not
useful.
"I have never done anything useful. No discovery of mine has made, or is likely to make, directly or indirectly, for good or ill, the least difference to the amenity of the world."

Godfrey Harold Hardy (1877-1947), left, and Paul Erdős (1913-1996), right. Hardy was the mentor of number theory marvel, Srinivasa Ramanujan. Erdős was an obsessive mathematician who devoted every waking hour to mathematics. (Left image, and right image, via Wikimedia Commons and modified for artistic effect.)
The apparent rules for beauty in a mathematical proof, as compiled on
Wikipedia, are as follow:
· A proof that uses a minimum of additional assumptions or previous results.
· A proof that is unusually succinct.
· A proof that derives a result in a surprising way (e.g., from an apparently unrelated theorem or collection of theorems).
· A proof that is based on new and original insights.
· A method of proof that can be easily generalized to solve a family of similar problems.
Supposedly
ugly proofs involve
laborious calculations (
computer-assisted proofs probably fall into this category), approaches that are either very conventional or overly elaborate, and ones that require too many
axioms or the results of previous ugly proofs.
Eccentric, but
eminent, mathematician,
Paul Erdős (1913-1996), had an interesting idea, called
Proofs from 'The Book'. "The Book" was the place in which
God had written the best and most elegant mathematical proofs. It was high praise when Erdős said that a proof was from The Book.
Do ordinary people experience mathematics
aesthetically like mathematicians and scientists? Three studies by scientists at the
University of Bath School of Management and the
Department of Mathematics of
Yale University provide evidence that they do.[5-7] According to these studies, average
Americans can relate to beautiful mathematical arguments in the same way that they can relate to art or
music. Three hundred individuals were in
approximate agreement about the particular way that four different proofs were beautiful.[6]
In his "Apology," Hardy specified some
qualities of mathematical beauty, and these were generalized by the study authors into the categories of
seriousness,
universality,
profundity,
novelty,
clarity,
simplicity,
elegance,
intricacy, and
sophistication.[6] According to one of the three studies, a high rating for elegance in both art and mathematical arguments closely predicted a high rating for beauty.[6] The three studies assessed the following:[5]
· The similarity of simple mathematical arguments to landscape paintings.
· The similarity of simple mathematical arguments to pieces of classical piano music.
· The commonality of reasons for the feeling of beauty for artworks and mathematical arguments.
In the first study, individuals were asked to match four mathematics proofs to four landscape paintings based on how aesthetically similar they found them. The proofs were the
sum of an
infinite geometric series, a
method for summing a sequential list of positive integers attributed to a youthful
Carl Friedrich Gauss, the
pigeonhole principle, and a geometric proof of a
Faulhaber formula.[6] The landscape paintings were "
Looking Down Yosemite Valley, California" by
Albert Bierstadt, "
A Storm in the Rocky Mountains, Mt. Rosalie" by Albert Bierstadt, "
The Hay Wain" by
John Constable, and "
The Heart of the Andes" by
Frederic Edwin Church.[6]
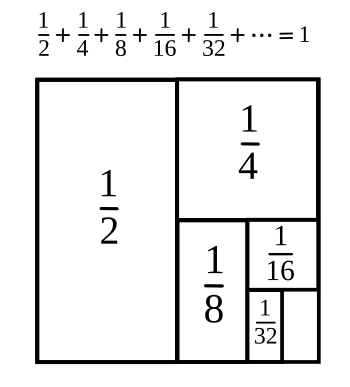
A geometric determination of the sum of an infinite series, one of the four mathematical arguments used in the study.
(Created using Inkscape. Click for larger image.)
For the second study, the mathematical proofs were the same, and the classical piano music pieces were
Franz Schubert's "
Moment Musical No. 4, D 780 (Op. 94),"
Johann Sebastian Bach's "
Fugue from Toccata in E Minor (BWV 914),"
Ludwig van Beethoven's "
Diabelli Variations (Op. 120)," and
Dmitri Shostakovich's "
Prelude in D-flat major (Op.87 No. 15)."[6] The third study asked another group of participants to rate, on a scale of zero to ten, the beauty of each of the four artworks and mathematical arguments as well as scoring them in the nine categories listed above.[6]
The overall results demonstrated a considerable
consensus among average people in the comparison of math and art, and somewhat less of a consensus in the judgment of classical piano music and mathematics.[7] As
Samuel G.B. Johnson, a study
author and a
Lecturer at the the University of Bath School of Management, summarizes,
"Laypeople not only had similar intuitions about the beauty of math as they did about the beauty of art, but also had similar intuitions about beauty as each other. In other words, there was consensus about what makes something beautiful, regardless of modality...There might be opportunities to make the more abstract, more formal aspects of mathematics more accessible and more exciting to students... and that might be useful in terms of encouraging more people to enter the field of mathematics."[7]
References:
- Melissa Hogenboom, "You decide: What is the most beautiful equation?" BBC, January 20, 2016.
- Massimo Pigliucci, "Richard Feynman was wrong about beauty and truth in science," Aeon, June 28, 2019.
- Sabine Hossenfelder, "Beauty is truth, truth is beauty, and other lies of physics," Aeon, July 11, 2018.
- Sabine Hossenfelder, "Lost in Math: How Beauty Leads Physics Astray," Basic Books (June 12, 2018), 304 pp., ISBN-13: 978-0465094257 (via Amazon).
- Samuel G.B. Johnson and Stefan Steinerberger, "Intuitions about mathematical beauty: A case study in the aesthetic experience of ideas," Cognition, vol. 189 (August 2019), pp. 242-259, https://doi.org/10.1016/j.cognition.2019.04.008.
- Kendall Teare, "Study shows we like our math like we like our art: beautiful," Yale University Press Release, August 7, 2019.
- People can see beauty in complex mathematics, study shows, University of Bath Press Release, September 5, 2019.
Linked Keywords: Cicero; oration; memory; Latin adage; De gustibus non disputandum est; grammar; grammatical; translation; one man's trash is another man's treasure; abstract expressionism; abstract art; Pierre Brassau; painted by a monkey; beauty; abstract expressionalist; Mark Rothko (1903-1970); near-perpetual copyright; photograph; David Barrie; Flikr group; Wikimedia Commons; art; symmetry; science; mathematics; BBC; online poll; public; equation; physicist; mathematician; Pythagorean theorem; ranking of beautiful equations in science and mathematics (BBC); salary; worth his salt; Yang–Baxter equation; Wikipedia; Gnumeric; voting; voter; Dirac equation; mass; massive; spin-1/2; elementary particle; electron; theory; special relativity; quantum mechanics; antimatter; positron; Paul Dirac (1902-1984); Nobel Prize in Physics; Erwin Schrödinger (1887-1961); Schrödinger wave equation; Pythagoras (c.570-c.495 BC); Leonhard Euler (1707-1783); Euler's Identity; fundamental mathematical constants; e (mathematical constant); i (imaginary unit); π (mathematical constant); fundamental mathematical operation; addition; multiplication; exponentiation; Euler's formula; truth; Massimo Pigliucci; professor; philosophy; City University of New York; criticism; criticize; idea; simplicity; motivation; string theory; experiment; validation; falsifiability; mathematical beauty; art form; musical composition; mathematical proof; student; number theory; Number theorist; G. H. Hardy (1877-1947); book; A Mathematician's Apology; utility; useful; amenity; Paul Erdős (1913-1996; mentor; number theory; intellectual giftedness; Srinivasa Ramanujan; obsession; obsessive; sleep; waking hour; Wikipedia; axiom; assumption; succinct; formal proof; derive; theorem; manual labour; laborious; calculation; computer-assisted proof; eccentricity (behavior); eccentric; eminence; eminent; proofs from 'The Book'; God; aesthetics; aesthetically; University of Bath School of Management; Department of Mathematics; Yale University; United States; American; music; approximation; approximate; quality (philosophy); qualities; seriousness; universality; profundity; novelty; clarity; simplicity; elegance; intricacy; sophistication; landscape painting; classical music; piano; addition; sum; geometric series; infinite geometric series; method for summing a sequential list of positive integers; Carl Friedrich Gauss; pigeonhole principle; Faulhaber formula; Looking Down Yosemite Valley, California; Albert Bierstadt; A Storm in the Rocky Mountains, Mt. Rosalie; The Hay Wain; John Constable; The Heart of the Andes; Frederic Edwin Church; geometry; geometric; Inkscape; Franz Schubert; Moment Musical No. 4, D 780 (Op. 94); Johann Sebastian Bach; Fugue from Toccata in E Minor (BWV 914); Ludwig van Beethoven; Diabelli Variations (Op. 120); Dmitri Shostakovich; Prelude in D-flat major (Op.87 No. 15); consensus; Samuel G.B. Johnson; author; Lecturer; intuition.