| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Lottery Simulation
December 10, 2018
Lotteries have been a part of
human culture for most of
history. The
scientific term for
modern man is
homo sapiens, the
sapiens appellation meaning
wise. However, wise men,
scientists, and
statisticians don't play the lottery, but that doesn't deter other people from supporting the many
government lotteries. The largest payout for the
Powerball, a US lottery, is often more than $1 billion, but the
odds for this are 1 in 292,201,338. One way to reduce the odds is the
tactic used by an
engineer with whom I worked. He always bought two tickets to double his odds of winning.
Most lotteries are structured to allow the player to choose his own numbers, and people will play "
lucky numbers" that relate to their life's history. If a
physicist were to play the lottery, he has the advantage of having a group of
magic numbers from which to choose. A magic number is a number of
nucleons (
protons or
neutrons) that form a complete
nuclear shell. Such nuclei are especially
stable. These magic numbers are 2, 8, 20, 28, 50, 82, and 126, and they are included as
sequence A018226 in the
On-Line Encyclopedia of Integer Sequences).
The term "magic number" was apparently coined by Eugene Wigner. There are some isotopes that are doubly magic, having a magic number of protons and a magic number of neutrons, as shown in this figure. Double magic allows the existence of unlikely stable isotopes, such as calcium-40, the most abundant isotope of calcium. Calcium-40 has far fewer neutrons than expected. Lead-208 is the heaviest stable nuclide. (Created using Inkscape)
As I wrote in an
earlier article (Allen Telescope Array, April 26, 2011), there's a
joke about lotteries. It might be known to everyone, but I'll retell it, anyways.
A religious man prays to God each night that he will win the state lottery. He does this for many years, but he never wins. Finally, the exasperated man asks God in a prayer, "Why won't you let me win the lottery?" God replies, "I want you to win, but you never buy a ticket!"
My
father enjoyed playing the
New York Lottery in which three numbers from 0-9 were drawn. That's despite the state's small payout for the 1 in 1000 odds. As many who were not statistically-minded, he thought there was a way for him to "
beat the system." He
recorded each day's winning numbers looking for a
pattern of repeating digits, and he asked me to do an
analysis to determine what numbers he should play. I couldn't just dismiss the idea as absurd, so I did a careful
mathematical analysis to prove the point. He was disappointed, but I think he continued to play.
One sure way to beat the odds is to
rig the game to make certain that your numbers come up. That's what happened in the
1980 Pennsylvania Lottery scandal. This lottery was also a three digit game with the numbers
dramatically selected using numbered
ping pong balls blowing around in a
container. The
conspirators purposely
weighted all balls, except those for
4 and
6, with
white latex paint, and the lighter balls rose up to the top to the selection
volume. The number
666 was selected on the night of April 24, 1980. However, the
conspiracy was discovered and measures were put into place to
prevent such tampering.
A much more serious lottery problem happened in 1969. On December 1, 1969, the
United States Selective Service System had a
draft (conscription) lottery to determine the order in which men would be called for
military service in the
Vietnam War. This lottery involved
printing all
dates of a year (366, since
leap year day was included), stuffing them individually into
opaque plastic capsules,
mixing them in a
box, pouring them into a
glass jar, and then pulling them individually. First picked were first called for military service; so, it was a very important lottery.
After the dates were pulled, it was found that dates late in the year were pulled earlier, and dates early in the year were pulled later. This was likely a consequence of the box having been loaded
month-by-month, starting with
January and ending with
December, and the
randomization effort being ineffective.
Computer simulation showed that the
probability distribution of dates was very unlikely.
A recent lottery story had a happy outcome for one
New York City man, Robert Bailey, who won the largest jackpot in New York Lottery history, $343.8 million, by playing Powerball.[1-3] This was his share of the $687.8 million overall jackpot that was split with another winner in
Iowa.[2] To achieve such a win, Bailey matched all six of the numbers drawn. What makes his win the topic of this
blog article is that he had played the same numbers for more than 25 years. He got the numbers from a
family member, and he was faithful to his
strategy of playing just those numbers.
News reports highlighted his strategy, and many people will think that it was key to his success.[1-3]
Anyone
schooled in
statistics realizes that the odds of winning are unchanged between playing the same numbers against a
random set of numbers, or playing random numbers against a random set of numbers. We statisticians are likely to be far outnumbered by all the people who don't understand this and will now
emulate Bailey's strategy. In any case, an easy computer simulation proves our case.
I wrote a simulation program in the
C programming language to test these two strategies (
source code available
here). A simple three digit lottery is used with random numbers selected by the
KISS algorithm devised by
American mathematician and
computer scientist,
George Marsaglia (1924-2011).[4] I wrote about KISS in a
recent article (NIST Randomness Beacon, October 1, 2018). KISS produces
64-bit random numbers.[4]
The results of my simulation are as expected, with no real difference between the two lottery strategies. My program, which ran 1,000 iterations of 100,000,000 trials took 760
seconds on my
run-of-the-mill desktop computer, a 3600
MHz dual core Intel i3-4160 having 8
gigabytes of
memory running the 64-bit
Linux 4.15.0-39-generic x86_64 kernel. The results are summarized in the following figures.
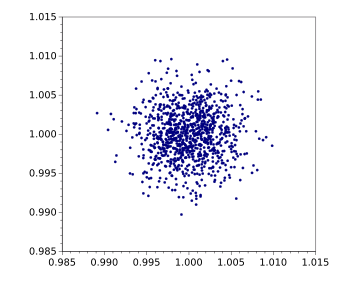
Lottery simulation results.
This is a scatterplot derived from the deviation from an ideal result in 1,000 successive simulations using each strategy in 100,000,000 trials.
An ideal result would have all points placed at (1.0,1.0). All the points fall within a percent of this ideal.
(Graphed using Gnumeric)
Histogram of the Lottery simulation.
This shows the distribution of the deviation of one lottery strategy over the other, and the results indicate much less than a 1% deviation for most trials.
The calculated standard deviation is 0.45%.
(Graphed using Gnumeric)
References:
- Robert Bailey, $343.8 Million Lottery Winner, New York City, New York Lottery Website, November 14, 2018.
- Faith Karimi, "New York man wins $344 million Powerball jackpot by playing same numbers for 25 years," WKTV Website, November 15, 2018.
- Georgett Roberts, "Meet the winner of the biggest lottery jackpot in New York history," New York Post, November 14, 2018.
- George Marsaglia, "64-bit KISS RNGs, The Coding Forums, February 28, 2009.
Linked Keywords: Lottery; human culture; history; science; scientific; modern man; homo sapiens; appellation; wisdom; wise; scientist; statistician; government; Powerball; odds; tactic (method); engineer; numerology; lucky number; physicist; magic number (physics); nucleon; proton; neutron; nuclear shell model; stable isotope; sequence A018226; On-Line Encyclopedia of Integer Sequences; Eugene Wigner; isotope; calcium-40; calcium; lead-208; nuclide; Inkscape; joke; religion; religious; God; state lottery; prayer; lottery ticket; father; New York Lottery; beat the system; diary; record; pattern; analysis; mathematical; cheating; rig; 1980 Pennsylvania Lottery scandal; drama; dramatically; ping pong ball; turbulence; blowing around; container; conspiracy; conspirator; weight; weighted; white; acrylic paint; latex paint; volume; tamperproofing; United States Selective Service System; draft lottery (1969); conscription; military service; Vietnam War; printing; calendar date; leap year day; opacity (optics); opaque; plastic; capsule (geometry); mixing; box; glass jar; month-by-month; January; December; randomness; randomization; computer simulation; probability distribution; New York City; Iowa; blog; family member; strategy; media (communication); news reports; education; schooling; statistics; random; set (mathematics); imitation; emulate; C programming language; source code; lottery.c; KISS algorithm; American; mathematician; computer scientist; George Marsaglia (1924-2011); 64-bit computing; second; run-of-the-mill; desktop computer; MHz; dual core; Intel i3-4160; gigabyte; dynamic random-access memory; Linux 4.15.0-39-generic x86 64; kernel; scatterplot; deviation (statistics); Gnumeric; histogram; strategy; standard deviation.