Great Circle Routes
June 25, 2018
While the
mathematics,
science, and
grammar I was taught in
elementary school were very useful in my life, I often wonder about the utility of some of the other topics in my
curriculum. It seemed that a primary purpose in
teaching was to keep
students continually occupied; and, when you run out of useful things to teach children in a particular age group, you teach some
random concept that they might also understand.
One such random piece of knowledge I was taught was the concept that
aircraft will travel a minimum distance between points on
Earth when they travel what are called
great circle routes. It seemed to me that this was one concept that would never be useful unless I became a
pilot. In retrospect, great circle routes must have been an attempt to impart some knowledge of
spherical geometry to elementary school students. Aircraft routing was one of its few examples, another being
sailing ships.
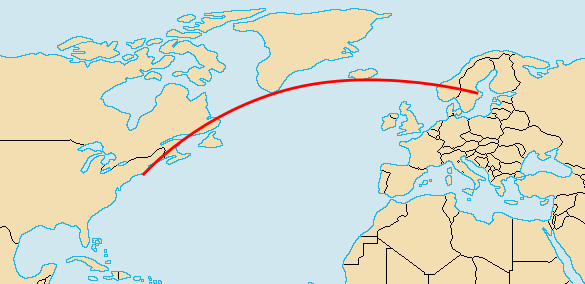
The great circle route between Stockholm, Sweden, and New York City, as shown on a portion of a Robinson projection map of the world. (Map image by Vardion, via Wikimedia Commons. Great circle route data by Poxnar from his map at Wikimedia Commons. Image created using Inkscape.)
Since great circles are the shortest distance between points on a
sphere, the
interior angles of
a triangle drawn on a sphere will sum to greater than 180
degrees (see this
Wikimedia Commons example). Preeminent
physicist,
Carl Friedrich Gauss (1777-1855), knew this fact quite well, as he performed a
geodetic survey of the
Kingdom of Hanover by
meshing together surveyed triangles. He was aided in this by his
invention of the
heliotrope, a focused sunlight version of a modern
laser pointer.
Gauss supposedly discovered
non-Euclidean geometries, a consequence of the arbitrariness of
Euclid's parallel postulate. Since Gauss had not
published, this discovery is ascribed to
János Bolyai, who published in 1832. Although we didn't know until the
20th century that
space curves in the presence of a gravitational field, Gauss actually did an
experiment in the 1820s to see if space was Euclidian.
It's unclear, however, whether testing the curvature of space was the actual purpose of the experiment, or if the experiment was just a test of his
surveying instruments. We now know that the effect is quite small, amounting to just 0.1
picoradians.[1] Although paths on the surface of the Earth will curve, light rays in Euclidian space will travel in
straight lines, so a triangle formed by light rays in Euclidian space will have 180 degrees as the sum of its interior angles. Gauss did this experiment with his heliotrope using three high
mountains as the
vertices of his triangle (see figure).
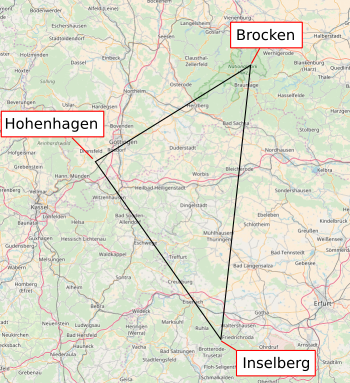
The three mountains of Gauss' triangle experiment, Brocken, Hohenhagen, and Inselberg.
This was a relatively huge triangle having sides of length 69, 85 and 107 kilometers.[2]
The Gauss heliotrope must have been powerful to be effective over such distances.
(Click for larger image. Map image from OpenStreetMap.org. Created using Inkscape.)
There are a few arguments that Gauss didn't intend this experiment as a test of the
geometry of space. One of these, by
mathematician,
John Conway, argues that any effect apparent on such a length scale on Earth would have been noticed by
astronomers many years prior.[2-3] Indeed, astronomer,
Ole Christensen Rømer (1644-1710) had discovered that the
speed of light was
finite in
observations of the satellites of Jupiter in 1676, long before Gauss' time. However, as an
experimenter myself, I know that when the
tools are at hand, it's hard to resist that fast-and-dirty experiment. You never know what you might find.
The Earth has some large
continents, and its
surface area is 71%
ocean. You can travel quite far on land, and you can
circumnavigate the Earth on sea, but what are the longest great circle paths on each? In 2012, Patrick Anderson, an
environmental law attorney, popularized a
conjecture that the longest great circle path on sea would be a 32,089.7
kilometer (19,939 mile) trip eastward from
Pakistan, snaking under
Africa and
South America, to
northeastern Russia.[5-7] As Anderson admits, he didn't discover that path, he merely found the starting and ending
coordinates on a
Wikipedia entry for
Extreme points of Earth, mapped the great circle, and published a
video.[5]
Neither Anderson nor the Wikipedia entry gave any evidence as to how this route was calculated, a definite Wikipedia example of
Citation Needed.[8] It's a long route; but, is it correct, and is there any longer route? Also, there's the question as to what such a route would be for land; that is, the longest great circle route that's uninterrupted by
lakes or seas.[6] This, of course, is a problem made for
computer analysis, so
Rohan Chabukswar from
United Technologies Research Center Ireland, and
Kushal Mukherjee from
IBM Research India, decided to tackle it.[4-8] To do this in a
non-brute-force method necessitated an
efficient algorithm.[4-8]

A cartoon from Randall Munroe's xkcd Comics, licensed under a Creative Commons Attribution-NonCommercial 2.5 License. (xkcd comic 285.)
The required
map dataset of the Earth's surface came from the
US National Oceanic and Atmospheric Administration's ETOPO1 Global Relief model. This model contains features of the entire
planet at a
spatial resolution of approximately 1.8 kilometers.[5] This means that you can miss quite a large body of water on land, or a very small
island at sea, but it's the best that can be done at present. Since the dataset also includes
altitude, it was easy to see whether or not you were at
sea level.[5]
A brute-force attempt using data at this resolution would involve 233,280,000 possible great circles, each containing 21,600 points. In such a
calculation, 5,038,848,000,000 data points would need to be examined.[5-6,8] Chabukswar and Mukherjee instead used an optimization algorithm called
branch-and-bound that examines only the most promising routes from an initial screening.[4-8] The resulted in a greatly diminished computation time, 10 minutes for the water path, and 45 minutes for the land path on a standard
laptop computer.[6-8] Their great circle route for a journey by sea matched Andersen's path.
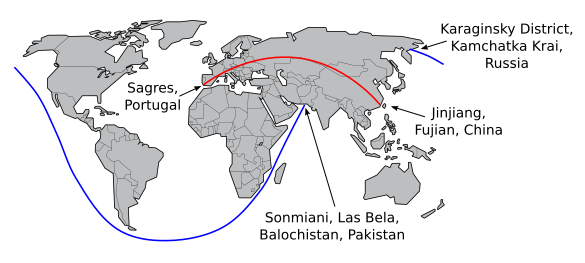
Longest land and sea great circle routes on Earth. (Simplified world map by Tom-b, via Wikimedia Commons. Image created using Inkscape from data in ref 4. Click for larger image.)[4]
The land path that avoids large bodies of water, but not
rivers, was a 11,241.1 kilometer trek through fifteen countries. It ran from a place near
Jinjiang, Fujian, China, and proceeds through
Mongolia,
Kazakhstan,
Russia, and
Europe. In Europe, it passed through
Poland, the
Czech Republic,
Germany,
Austria,
Liechtenstein,
Switzerland,
France, and
Spain, finally finishing near
Sagres, Portugal.[5-6,8] If you wanted to take this path, you would need to take some major
detours to traverse
bridges.[8]
The starting and ending locations are listed in the table. Two questions remain; namely, who did the initial Wikimedia posting, and when will someone complete the sea trip?[6]
References:
- J. B. Hartle, "Gravity: An Introduction to Einstein’s General Relativity," Addison-Wesley, January 5, 2003, ISBN: 9-780-80538-662-2, via Amazon, as quoted in ref. 2.
- Peter Lynch, "Gauss's Great Triangle and the Shape of Space, ThatsMaths Web Site, July 10, 2014.
- John H. Conway, "Gauss and the really large triangle," MathForum, 1998.
- Rohan Chabukswar and Kushal Mukherjee, "Longest Straight Line Paths on Water or Land on the Earth," arXiv, April 9, 2018.
- David Shultz, "This ocean path will take you on the longest straight-line journey on Earth," Science, April 30, 2018, doi:10.1126/science.aau0354.
- Computer scientists have found the longest straight line you could sail without hitting land, Technology Review, April 30, 2018.
- Natasha Frost, "Scientists Have Confirmed the Longest Straight Line Over Water," Atlas Obscura, May 1, 2018.
- George Dvorsky, "This Is the Longest Straight Path You Could Travel on Water Without Hitting Land," Gizmodo, May 2, 2018.
Linked Keywords: Mathematics; science; English grammar; elementary school; curriculum; education; teaching; student; randomness; random; aircraft; Earth; great-circle navigation; great circle route; aircraft pilot; spherical geometry; sailing; Stockholm, Sweden; New York City; Robinson projection; Vardion; Wikimedia Commons; Poxnar; Inkscape; sphere; interior angle; triangle; degree of angle; physicist; Carl Friedrich Gauss (1777-1855); geodesy; geodetic; surveying; survey; Kingdom of Hanover; polygon mesh; meshing; invention; heliotrope; laser pointer; non-Euclidean geometry; Euclid; parallel postulate; cademic publishing; published; János Bolyai; 20th century; general relativity; space curves in the presence of a gravitational field; experiment; surveying instrument; picoradian; straight line; mountain; vertex (geometry); vertices; Gauss' triangle experiment; Brocken; Hoher Hagen (Dransfeld); Hohenhagen; Inselberg; kilometer; heliotrope; OpenStreetMap; geometry; mathematician; John Horton Conway; astronomer; Ole Christensen Rømer (1644-1710); speed of light; finite; observations of the satellites of Jupiter; experimenter; scientific instrument; tool; continent; surface area; ocean; circumnavigation; circumnavigate; environmental law; lawyer; attorney; conjecture; kilometer; Pakistan; Africa; South America; northeastern; Russia; location (geography); coordinate; video; Citation Needed; lake; computer; analysis; Rohan Chabukswar; United Technologies Research Center Ireland; Kushal Mukherjee; IBM Research India; proof by exhaustion; brute-force method; algorithmic efficiency; algorithm; cartoon; Randall Munroe; xkcd Comic; Creative Commons Attribution-NonCommercial 2.5 License; xkcd comic 285; map; dataset; US National Oceanic and Atmospheric Administration; ETOPO1 Global Relief model; planet; angular resolution; spatial resolution; island; altitude; sea level; calculation; laptop computer; river; Jinjiang, Fujian, China; Mongolia; Kazakhstan; Europe; Poland; Czech Republic; Germany; Austria; Liechtenstein; Switzerland; France; Spain; Vila do Bispo; Sagres, Portugal; detour; bridge; latitude; longitude; Karaginsky District, Kamchatka Krai, Russia; Balochistan, Pakistan; Jinjiang, Quanzhou, Fujian, China.