The Sofa Problem
May 1, 2017
My
elementary school mathematics courses included light introductions to
trigonometry,
geometry, and
number theory. One problem that I remember had an illustration of a practical problem with a mathematical solution. A boy wanted to bring his
model airplane through a
door, but he was having problems. The plane, which would fit inside a perfect
square, wouldn't pass through in the common configurations of
wings parallel to the ground, and wings
perpendicular to the ground. It was our task to see whether the boy could ever get the model airplane through the door.
As can be seen in the figure,
rotating the containing square would work; provided, however that the width of the doorway was compatible with the airplane length, a
diagonal of the square. Happily, the length of the airplane was slightly less than
√2 times the width of the doorway. Left unsaid was why the boy didn't just rotate the airplane to take advantage of its thinner
profile in the other direction. Perhaps his
smarter sister would have done that.
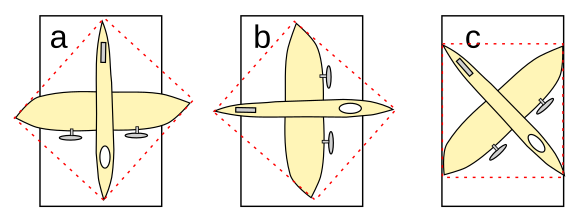
Thou shalt not pass. The model airplane, which fits inside a square, is too wide to pass through a doorway in configurations a or b, but it will pass in configuration c, provided that it's length is not larger that the width of the doorway times the square-root of two. (Inkscape.)
A similar problem, called the
Kakeya needle problem, was mentioned in a recent article by
Evelyn Lamb of the
University of Utah in her
Roots of Unity blog at the
Scientific American web site.[1] This problem, posed in 1917 by
Japanese mathematician,
Sōichi Kakeya, concerns the minimum
area in the
plane in which a
needle can be turned through 360°. One example of such turning is shown in the figure.
Kakeya needle example.
(Wikimedia Commons graphic by Claudio Rocchini.)
The object of Lamb's article was a
sailing ship, and not an airplane. The Kakeya needle problem relates to the ship, since the long
mast of a sailing ship approximates a needle. The example she cites is the removal of a display ship from a
Paris outdoor
exhibit with the necessary avoidance of
trees,
sculptures, and other nearby objects. The
crew that removed the ship were likely heartened by the idea that, if it was put where it was, then it could likewise be removed, and this was accomplished successfully with the proper
rigging.
While most people are not likely to be moving sailing ships, they do move a lot of bulky
furniture in their
homes. In my own home, we have a massive
sofa bed in the
living room, and we still can't believe that the
movers were somehow able to bring it through our front door, around a
corner, and into the room. As it turns out, the "
moving sofa problem" has been on mathematicians' minds for quite some time. Simply stated, the moving sofa problem asks what
planar shape of maximal
area can move around a
right-angled corner in a
hallway of
unit width.[2-5]
The problem is simplified by limiting movement within a plane, so the
tilting tricks of actual movers cannot be employed. The problem was posed by
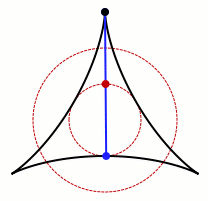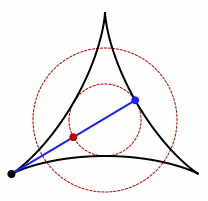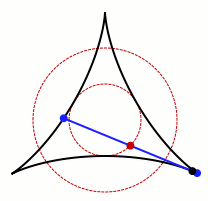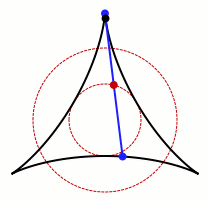
Leo Moser in 1966.[6] A
semicircle of area
π/2 (1.57) will traverse a right-angled corner in a corridor of unit width, but there are shapes that will do that with a larger area.
One such shape with an area of 2.2195 was devised by Gerver in 1992, and it is
conjectured to be the solution of largest area (see figure).[7] Gerver's shape is formed from eighteen
curves, each defined by an
equation. The sofa problem has been revisited by
Dan Romik, a
professor in the
Department of Mathematics,
University of California Davis, as the "
ambidextrous sofa problem" in which the object must traverse both a right- and left-angled corner. Surprisingly, Romik's shape is formed, also, from eighteen curves.

Gerver's sofa, which has an area of 2.2915, expressed in units of the corridor width.
This sofa will only navigate around right-angled corners.
(Modified Wikimedia Commons image by "Weburbia.")
Romik was inspired to investigate the problem through his
hobby of
3-D printing. Says Romik, "I'm excited by how 3-D technology can be used in math... Having something you can move around with your
hands can really help your
intuition."[4] As Romik
translated Gerver's
equations into
code that a 3-D printer could understand, he became interested in the mathematics of the solution. This inspired Romik to try his hand at developing new equations and refining them through
computer code.[4]
In April, 2016, Romik decided to shift his attention to the ambidextrous moving sofa problem, a problem previously investigated by
John Horton Conway and others.[2-3,5] Assisted by
software, Romik found a
dumbbell-shaped object that worked (see figure). The final object has an area of 1.64495, which might be the largest possible area for an ambidextrous moving sofa.[5] Says Romik, "I remember sitting in a
café when I saw this new shape for the first time... It was such a beautiful moment."[4]
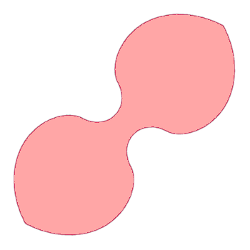
Romik's ambidextrous moving sofa.
This object has an area of 1.64495521, expressed in units of the corridor width.
(Modified Wikimedia Commons image by "Weburbia.")
Gerver conjectured that his shape is the shape of maximal area that solves the right-angled corner sofa problem, and no one has discovered an object of larger area since Gerver's 1992 paper.[5] Romik points out, however, that there is no
proof that this is the case, and there's always the possibility that an object of larger area will be found. "It's a surprisingly tough problem... It's so simple you can explain it to a
child in five minutes, but no one has found a proof yet."[4]
Romik has one advantage over Gerver, since his ambidextrous sofa is defined by a
closed form solution that's defined by equations that don't contain any
arbitrary constants. It differs in that respect from previous ambidextrous sofas designed by Kiyoshi Maruyama in 1973 and Philip Gibbs in 2014.[5] The area of Romik's sofa is equal to
X + arctan(Y), where
X and
Y are solutions of the
cubic equations,
x2(x+3) = 8 and
x(4x2 + 3) = 1, respectively.[2-3]

Nicely pivoted.
The illustration shows successive images of a Romik ambidextrous sofa moving down a corridor with a right- and left-angled turn.[8]
(Drawn using Inkscape.)
![]()
References:
- Evelyn Lamb, "The Serenity of Kakeya," Roots of Unity blog on Scientific American. February 27, 2017.
- Dan Romik, "Differential Equations and Exact Solutions in the Moving Sofa Problem," Experimental Mathematics, Advanced Online Publication (15 pages), January 19, 2017, http://dx.doi.org/10.1080/10586458.2016.1270858.
- Dan Romik, "Differential equations and exact solutions in the moving sofa problem," arXiv, July 11, 2016. A PDF file can be found here.
- Becky Oskin, "New Twist on Sofa Problem That Stumped Mathematicians and Furniture Movers," University of California Blogs, March 20, 2017.
- Dan Romik's page on the moving sofa problem (with animations and 3-D printer files).
- Leo Moser, "Moving furniture through a hallway," SIAM Rev., vol. 8, no. 3 (1966), p. 381, DOI:10.1137/1008074.
- Joseph L. Gerver, "On moving a sofa around a corner," Geometriae Dedicata, vol. 42, no. 3 (June, 1992), pp. 267-283, DOI: 10.1007/BF02414066.
- Animation of Romik's ambidextrous sofa moving through a corridor.
Permanent Link to this article
Linked Keywords: Elementary school; mathematics; course; trigonometry; geometry; number theory; model airplane; door; square; wing; parallel; perpendicular; rotation; rotating; diagonal; square root of 2; profile; intelligence; smart; sibling; sister; model airplane; square; Inkscape; Kakeya needle problem; Evelyn Lamb; University of Utah; Roots of Unity blog; Scientific American; web site; Japanese; mathematician; Sōichi Kakeya; area; plane; needle; Wikimedia Commons; sailing ship; mast; Paris; exhibit; tree; sculpture; crew; rigging; furniture; home; sofa bed; living room; moving company; mover; corner; moving sofa problem; plane; planar; area; clockwise; right-angled; hall; hallway; unit vector; tilt; tilting; Leo Moser; semicircle; conjecture; curve; equation; Dan Romik; professor; Department of Mathematics; University of California Davis; ambidexterity; ambidextrous; hobby; 3-D printing; hand; intuition; translation; translated; equation; source code; computer code; John Horton Conway; software; dumbbell-shape; coffeehouse; café; corridor; mathematical proof; child; closed form solution; arbitrariness; arbitrary; constant; cubic equations; pivoted; Inkscape.