| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Voronoi Tessellation
December 18, 2017
Students are taught much "useless information" while in
elementary school, most of which is concentrated in
history classes. Nearly all of these facts are forgotten; but, for some reason, a few
random facts linger in the dark recesses of
memory. For example, I remember that the
French military engineer,
Pierre Charles L'Enfant (1754-1825), was responsible for the
street plan of the United States Capital.
As most people, I memorize facts by
association. In this case, the association for a
child was easily formed, since the name, "L'Enfant," looks as if it should be pronounced like "
elephant." If I had known a little more
French at the time, the association might have been different, perhaps a
diapered George Washington. L'Enfant's plan had the familiar
rectangular grid layout of the
streets with some
diagonal avenues that intersected some grid points at
circles and
plazas.
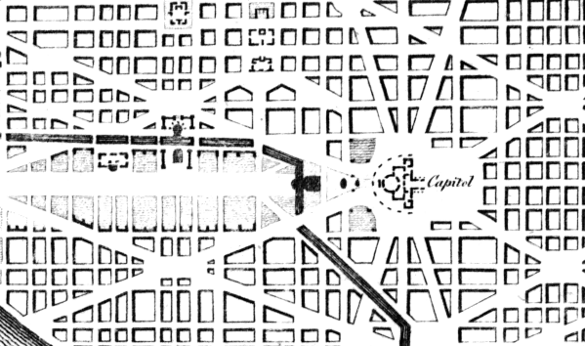
L'Enfant's plan for the area near the US Capitol building. A March, 1792, engraving on paper from the US Library of Congress, via Wikimedia Commons
Any division of a plane with
geometric shapes such as this is a
tessellation. The most common tessellation is
tiling with regular polygons, as exists in many
patios. However, a common tessellation in
scientific studies is the
Voronoi tessellation, one example of which is the decomposition of a
lattice into
Wigner-Seitz cells.
Wigner-Seitz tessellation, used in the analysis of
crystal symmetry, is named after
physicists,
Eugene Wigner and
Frederick Seitz. The construction of this tessellation is quite simple. You just draw
perpendicular lines at the midpoints of the lines that connect
nearest-neighbor atoms, as shown in the figure. Such a construction isn't limited to
two dimensions. In a
three-dimensional lattice, you can just as easily construct
planes at the midpoints to get a
volumetric cell.
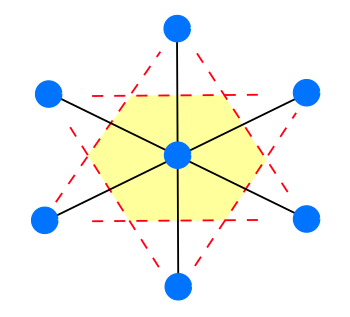
Procedure for construction of a Wigner-Seitz cell.
1. Draw connecting lines between nearest-neighbors
2. Construct perpendicular lines at the midpoints.
3. The area bounded by these lines is a Wigner-Seitz cell.
(Created using Inkscape)
One interesting example of Voronoi tessellation is the study done in 1854 by the
British physician,
John Snow (1813-1858) who partitioned an area of
cholera outbreak. He created this tessellation around individual public
water pumps, so the generated cells represented the areas closest to each pump. In this fashion, he isolated the source of the
infection to a particular public pump at
Broad Street.
Since a Voronoi cell is defined as all points that are closer to the cell focus point than any other focus point, it's easily seen that a Voronoi tessellation of a two-dimensional
simple cubic lattice results in a
hexagonal tiling (see figure).
Voronoi tessellation of a two-dimensional simple cubic lattice, resulting in a hexagonal tiling.
(Created using Inkscape)
One method of creating a Voronoi tessellation deserves special mention. That's
Fortune's algorithm, an
efficient method devised in 1986 by
Steven Fortune, a
distinguished member of the technical staff at
Bell Labs.[1] His
algorithm, and several others, are hosted on
CGAL, the Computational Geometry Algorithms Library web site.[2]
Fortune's algorithm, while efficient, is not
intuitive. A more understandable approach is to generate expanding
circles around the focus points that bump up against each other. This approach is nicely illustrated in the following figure that was generated using
MATLAB.
Voronoi tessellation created by Euclidian growth.
The MATLAB source code for creation of this demonstration image can be found here.
(Wikimedia Commons image by Jahobr, a prolific contributor to Wikimedia Commons)
MATLAB is
proprietary software. Since I'm an advocate of
free and open-source software, and I needed a little coding practice, I decided to write a
C language program to accomplish Voronoi tessellation using this expanding circles approach (source code
here.) Since I'm not a
professional programmer, this code most certainly could be improved, but it produces the desired result.
The program outputs a
*.tga image, a
file format chosen because it's easy to implement. The following image is a honeycomb generated from a simple cubic lattice.
Voronoi tessellation on a simple cubic grid, as generated by my C language program.
![]()
The following are two Voronoi tessellations generated from random focus points.
Voronoi tessellations generated from random focus points.
References:
- S. Fortune, "A sweepline algorithm for Voronoi diagrams," Algorithmica, vol. 2 (November, 1987), p. 153ff., https://doi.org/10.1007/BF01840357.
- Voronoi Diagrams section of the Computational Geometry Algorithms Library.
Linked Keywords: Student; elementary school; history; classroom; class; randomness; random; memory; France; French; military engineering; military engineer; Pierre Charles L'Enfant (1754-1825); L'Enfant Plan; street plan of the United States Capital; associative memory (psychology); association; child; elephant; French language; diaper; diapered; George Washington; rectangle; rectangular; regular grid; street; diagonal; avenue; traffic circle; plaza; engraving; paper; US Library of Congress; Wikimedia Commons; geometry; geometric; tessellation; tiling with regular polygons; patio; science; scientific; Voronoi tessellation; Bravais lattice; Wigner-Seitz cell; crystal symmetry; physicist; Eugene Wigner; Frederick Seitz; perpendicular; nearest-neighbor; atom; two-dimensional space; three-dimensional space; plane; volume; volumetric; Wigner-Seitz cell; Inkscape; Great Britain; British; physician; John Snow (1813-1858); cholera; water pump; infection; 1854 Broad Street cholera outbreak; simple cubic lattice; hexagonal tiling; Fortune's algorithm; big O notation; Steven Fortune; distinguished member of the technical staff; Bell Labs; algorithm; CGAL, the Computational Geometry Algorithms Library; intuition; intuitive; circle; MATLAB; Euclidean geometry; source code; Jahobr; proprietary software; free and open-source software; C language program; voronoi.c; professional; programmer; Truevision TGA; *.tga image; file format.