Income Inequality and Geometrical Frustration
March 20, 2017
We've all been
frustrated by events in our personal lives. As
children, we never received that one special
toy that we really wanted. As
adults, we wonder if that
red light will ever change; or, if we'll ever have enough
money saved for a
down payment on a
house.
Physicists are likewise frustrated by things like
peer review, but they have a more
scientific understanding of frustration.
Just as in personal frustration, when a goal is blocked by some situation,
geometrical frustration involves a goal, typically descent into the
lowest energy state, that's blocked by a competing requirement of a necessary
spatial arrangement of objects. One simple example of this is found when trying to establish an
antiferromagnetic ordering of
spins on a
triangular lattice.
In 1924,
German physicist,
Ernst Ising (1900-1998), did his
thesis on a
model of
magnetism involving
nearest neighbor interaction between spins arrayed in a
straight line. This model was subsequently generalized to a
two-dimensional lattice by
Lars Onsager (1903-1976), who was awarded a
Nobel Prize in Chemistry in 1968 for his contributions to the
thermodynamics of
irreversible processes.
In antiferromagnetic ordering, near-neighbor spins should be
antiparallel, and this is easy to do on a
square lattice. As the figure shows, when we try to do this on a triangular lattice, we're frustrated, since one spin is necessarily parallel to a neighbor spin in any triangle.
G.H. Wannier (1911-1983), known especially among
condensed matter physicists for his
eponymous Wannier functions,
calculated the residual
entropy at
absolute zero of spins on such a triangular lattice as 0.3383
R, or about 0.67
cal/
K/
mol.
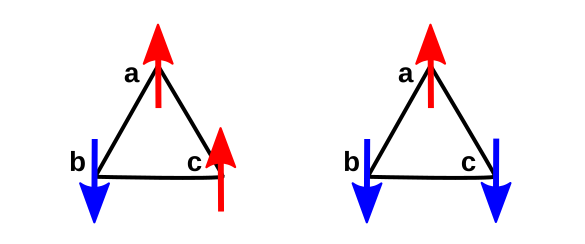
Attempted antiferromagnetic ordering on a triangular lattice. Only two of the three spin pairs can be aligned antiparallel on any triangular unit cell. (Created using Inkscape.)
Much earlier than that,
Linus Pauling used geometrical frustration to explain the residual entropy of
ice.[2]
Solid water H2O, exists as
oxygen anions surrounded by four
protons, any two of which can be in closer proximity to form the water
molecule, an arrangement commonly known as the
ice rules. Pauling found the number of possible arrangements
Ω of particles in the
ground state of an
ensemble of
N ice molecules to be
Ω < 22N(6/16)N.
Calculating the
Boltzmann entropy from this yields the following:
S = kBln(Ω) = NkBln(3/2) = 0.81 cal/K/mol,
where k
B is the
Boltzmann constant. This value agrees closely with an
experimental value of 0.82 ± 0.05 cal/K/mol.[3]
Ludwig Boltzmann (1844-1906) applied such
statistics to thermodynamics in 1875, and he used statistics to explain the
probability distribution of
speeds of molecules in a
gas, now called the
Maxwell–Boltzmann distribution, that was first investigated by
James Clerk Maxwell (1831-1879) in 1860. What's surprising is that the distribution of incomes follows this same curve. I reviewed this idea that "people are like gas" in an
earlier article (The Entropy of Nations, January 22, 2014)
Such a correspondence would be just an
analogy without a
mechanism; and, just as gas molecules exchange
energy when they meet each other, people exchange
wealth. The precise distribution of wealth is generated by fine-tuning the degree of wealth transferred at
random meetings. The idea that we're being guided by such an "
invisible hand" is exemplified by the following
graph that shows the
partitioning of
wealth between the many and the few in the
United States for the
year 2000. Such studies are now a routine part of a field known as
econophysics.
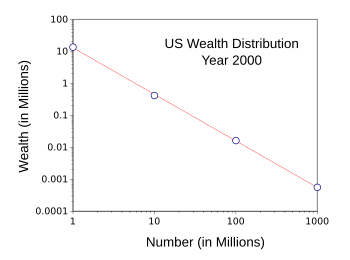
US wealth distribution for the year 2000.
Such regularity in data suggests a simple mechanism.
(Data from ref. 4, graphed using Gnumeric.)
Two
scientists affiliated with
Los Alamos National Laboratory (Los Alamos, New Mexico), and a visiting scientist from the
Université Paris Saclay (Gif-sur-Yvette, France) have recently published a statistical
model in which they've applied geometrical frustration to a simple
social network. They show how
income inequality can arise in such a system, but also how constraints on interactions between
agents can lead to greater income equality.[5-6]
The model relates to the traditional
Horatio Alger rags-to-riches story, since it incorporates channels of wealth transfer that transcend
social stratification.[6] Says
Cristiano Nisoli, a member of the
Physics of Condensed Matter and Complex Systems group at Los Alamos and lead
author of the study,
"Most theories of wealth inequality rely on social stratification due to income inequality and inheritance... We consider, however, the possibility that in our more economically fluid world, novel, direct channels for wealth transfer could be available, especially for financial wealth."[6]
Income equality (a.k.a., "fairness in wealth distribution") is easily quantified by the
Lorenz curve and the
Gini coefficient. In the LANL model, an ensemble of agents has the ability to acquire wealth through transfer from other agents; and, having wealth gives an advantage of gaining more wealth, which is an obvious feature of nearly all
societies. Setting these agents loose in their
computer world leads to different wealth distributions depending on applied constraints.[6]
The "
law-of-the-jungle"
scenario, illustrated below where the allocation of opportunities does not change and wealth is acquired in a meeting of agents without any rules, leads to gross inequality. As Nisoli explains, "If driven by power alone, the market evolution reaches a
static equilibrium characterized by the most savage inequality." The opportunities to acquire wealth are concentrated in just a few agents, and these amass all the wealth of the society.[6]

The rich get richer. An example of the acquisition of wealth when the "law of the jungle" in which every agent (blue) can grab wealth (red circles) to fill available opportunities (white circles). (Fig. 1 of ref. 5, modified, licensed under a Creative Commons Attribution License)[5)]
When transactions of wealth are regulated such that people can gain or lose wealth from only neighbors in the network, fairness is considerably increased. With some tuning, there's an emergence of three
social classes,
lower,
middle, and
upper.[6] Just as in real life, an
unexpected economic event shifts the equilibrium to distort a previously stable class structure.[6] This research was funded by the
US Department of Energy.[5]
References:
- G. H. Wannier, "Antiferromagnetism. The Triangular Ising Net," Phys. Rev., vol. 79, no. 2 (July 15, 1950), pp. 357ff., DOI:https://doi.org/10.1103/PhysRev.79.357.
- Linus Pauling, "The Structure and Entropy of Ice and of Other Crystals with Some Randomness of Atomic Arrangement," J. Am. Chem. Soc., vol. 57, no. 12 (December, 1935), pp. 2680-2684, DOI: 10.1021/ja01315a102.
- W. F. Giauque and J. W. Stout, "The Entropy of Water and the Third Law of Thermodynamics. The Heat Capacity of Ice from 15 to 273K," J. Am. Chem. Soc., vol. 58, no. 7 (July 1, 1936), pp. 1144-1150, DOI: 10.1021/ja01298a023.
- James B. Davies, Anthony Shorrocks, Susanna Sandstrom and Edward N. Wolff, "The World Distribution of Household Wealth," escholarship.org web site (The University of California), July, 2007, p. 26.
- Benoit Mahault, Avadh Saxena, and Cristiano Nisoli, "Emergent inequality and self-organized social classes in a network of power and frustration," PLoS ONE, vol. 12, no. 2 (February 17, 2017), Article No. e0171832, doi:10.1371/journal.pone.0171832. This is an open access publication with a PDF file here.
- Science versus the Horatio Alger myth, DOE/Los Alamos National Laboratory Press Release, February 22, 2017.
Permanent Link to this article
Linked Keywords: Frustration; child; children; toy; adult; traffic light; red light; money; down payment; house; physicist; peer review; science; scientific; geometrical frustration; ground state; lowest energy state; three-dimensional space; spatial; antiferromagnetism; antiferromagnetic ordering; spin; triangle; triangular; lattice; Germany; German; Ernst Ising (1900-1998); thesis; Ising model; magnetic field; magnetism; nearest neighbor; straight line; two-dimensional; Lars Onsager (1903-1976); Nobel Prize in Chemistry; thermodynamics; irreversible processes; antiparallel; square; G.H. Wannier (1911-1983); condensed matter physicist; eponymous; Wannier functions; calculation; calculated; entropy; absolute zero; gas constant; R; calorie; cal; kelvin; K; mole; mol; unit cell; Wikimedia Commons; Linus Pauling; ice; solid; water; oxygen; anion; proton; molecule; ice rules; ensemble; Boltzmann entropy; Boltzmann constant; experiment; experimental; Ludwig Boltzmann (1844-1906); statistical mechanics; statistics; probability distribution; speed; gas; Maxwell–Boltzmann distribution; James Clerk Maxwell (1831-1879); analogy; process theory; mechanism; energy; wealth; randomness; random; invisible hand; Cartesian coordinate system; graph; equipartition theorem; partitioning; United States; year 2000; econophysics; data; Gnumeric; scientist; Los Alamos National Laboratory (Los Alamos, New Mexico); Université Paris Saclay (Gif-sur-Yvette, France); computer simulation; model; network theory; social network; economic inequality; income inequality; agent; Horatio Alger; rags-to-riches; social stratification; Cristiano Nisoli; Physics of Condensed Matter and Complex Systems group; author; inheritance; Lorenz curve; Gini coefficient; society; societies; computer simulation; law-of-the-jungle; scenario; equilibrium thermodynamics; static equilibrium; Creative Commons Attribution License; social class; lower class; middle class; upper class; financial crisis; unexpected economic event; US Department of Energy.