Smectic Martensite
May 5, 2016
One
phenomenon with which every
graduate student is familiar, independent of his field of study, is the fact that
professors will selectively emphasize in their teaching the topics with which they are most interested, or most familiar. That's why my
graduate course in
physical metallurgy had several
lectures devoted to
Ostwald ripening; and, why a course I had in
fracture mechanics had far too much information about
martensite, and the
martensitic transformation. I wrote about Ostwald ripening in an
earlier article (Is Religion becoming Extinct?, April 1, 2011).
As you've likely guessed, martensite is named after its discoverer, the
German metallurgist,
Adolf Martens (1850-1914). Martensite usually refers to an extremely
hard form of
steel possessing an unique
crystal structure, but the term is often used to describe other
alloys formed by a
martensitic transformation, a transformation forced to happen so quickly that the
atoms in the
material can't
diffuse into an
equilibrium state. For this reason, martensite is is not an equilibrium
phase; so, it does not appear on an
equilibrium phase diagram (see figure).
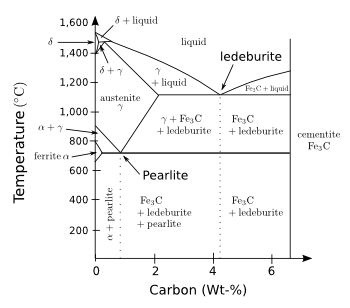
No Martensite here.
The iron-rich portion of the iron-carbon phase diagram.
(Modified Wikimedia Commons image by Christophe Dang Ngoc Chan.)
(Click for larger image.)
As the iron-carbon phase diagram above shows,
Fe3C (iron carbide, cementite) is an equilibrium phase formed when the
austenite (γ) phase is cooled below about 700
°C. If the cooling is too rapid, the carbon atoms are not able to diffuse through the solid to form cementite. Instead, they're locked into the
face-centered cubic lattice of austenite, which transforms into a
highly strained body-centered tetragonal form of
ferrite. Ferrite, as the phase diagram again shows, shouldn't have that much carbon, so it's
supersaturated with carbon and, therefore,
metastable.
Having too much carbon in a phase not capable of containing it is like trying to put
a square peg into a round hole, so something has to give. In this case, the material
deforms, creating a large number of
dislocations, and dislocations give steel its
strength. Martensitic steel can be nearly twice as hard as
pearlitic steel.
Since martensite is metastable, it will be lost with application of higher
temperature. A common
steelmaking technique is to create a steel with too much martensite, then
annealing it to produce enough martensite for the intended application. If martensite is so hard, why would you want to remove it? Hard materials are also
brittle, so you want your steel to be just hard enough, and not too brittle. That's why martensite was a topic in my fracture mechanics course.
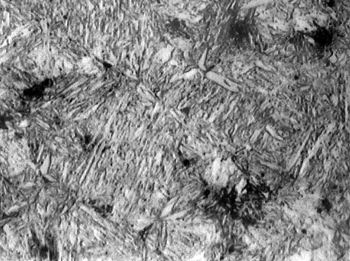
Metallograph of martensitic steel with 0.35% carbon, water-quenched from 870°C.
(Via Wikimedia Commons.)
The
grain structure of martensite appears also in
smectic-phase liquid crystals. In a recent paper in
Physical Review Letters,
physicists from
Cornell University (Ithaca, New York) have shown a connection between the smectic
microstructure, with its ordered patterns of
geometrically perfect
ellipses and
hyperbolas, and martensite.[1-2]
This type of microstructure arises when
nature needs to fill a
three-dimensional space with
conic sections under a specific set of
boundary conditions.[1] Interestingly, there's a similarity between the
mathematics required for this and the mathematics of
special relativity involved with
Lorentz transformations.[1]
The Cornell research team, led by physics professor,
James Sethna, calls smectic liquids "the world's weirdest martensite."[1-2] Their
computer modeling research made use of the extraordinary processing power available from the
graphics processing unit (GPU) integrated circuits normally used to speed
graphics for
video games. They developed a
clustering algorithm that demonstrated the similarity in the formation of the smectic liquid crystal and martensite microstructure.[2]
Says Sethna,
"This has been this puzzle for many years, and it finally has a suitably beautiful explanation... It ties together ideas from special relativity, and ideas from martensites, to explain this whole puzzle. It's aesthetically beautiful... there's a little bit of Euclidean geometry for those people who actually went to geometry class. It's like, 'Ellipses and hyperbolas, I remember those.' And you pour this (smectic) liquid and it forms these things."[2]

I would like to have this abstract art image hanging on my wall.
This is actually a simulation of a smectic microstructure.
(Cornell University image by the James Sethna Lab.)
The inspiration for this discovery came from an observation more than a
century ago by the
French physicist
Georges Friedel. In 1910, Friedel found that a fluid having equally spaced layers of
molecules will form ellipses and hyperbolas.[2] In filling three-dimensional space, concentric, equally spaced
spheres will form a point defect at the center. Another class of geometrical figures, the
cyclides of Dupin, will fill space with only ellipses and hyperbolas as defects. Friedel deduced the structure of his fluid by making the connection to the cyclides of Dupin.[2]
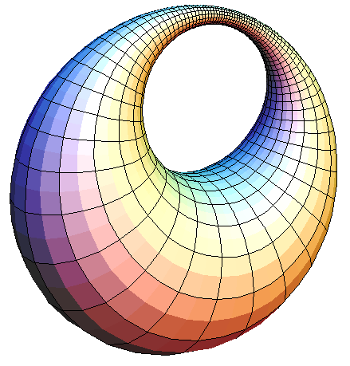
Ring cyclide generated by an inversion of a torus.
This image was generated in 2005, so you can see how far computer graphics has advanced since that time, aided by more powerful computers and GPU chips.
(Wikimedia Commons image by Xah Lee.)
Says Sethna, "Now we know that these cool cyclides follow the same rules as the crystals that fit together into martensitic steel."[2] This research was funded by the
U.S. Department of Energy and the
Simons Foundation.[2]
References:
- Danilo B. Liarte, Matthew Bierbaum, Ricardo A. Mosna, Randall D. Kamien, and James P. Sethna, "Weirdest Martensite: Smectic Liquid Crystal Microstructure and Weyl-Poincaré Invariance," Phys. Rev. Lett., vol. 116, no. 14 (April 8, 2016), article no. 147802, DOI:http://dx.doi.org/10.1103/PhysRevLett.116.147802.
- Daryl Lovell, "Weirdest martensite’: Century-old smectic riddle finally solved," Cornell University Press Release, April 14, 2016.
- Eric W. Weisstein, "Cyclide." From MathWorld--A Wolfram Web Resource.
Permanent Link to this article
Linked Keywords: Phenomenon; postgraduate education; graduate student; professor; graduate course; physical metallurgy; lecture; Ostwald ripening; fracture mechanics; martensite; diffusionless transformation; martensitic transformation; German; metallurgy; metallurgist; Adolf Martens (1850-1914); hardness; hard; steel; crystal structure; alloy; atom; material; diffusion; diffuse; thermodynamic equilibrium; phase; equilibrium phase diagram; iron; carbon; Wikimedia Commons; Christophe Dang Ngoc Chan; Fe3C (iron carbide, cementite); austenite; Celsius; °C; cubic crystal system; face-centered cubic; crystal structure; lattice; deformation; strain; tetragonal crystal system; body-centered tetragonal; ferrite; supersaturation; supersaturated; metastability; metastable; a square peg into a round hole; dislocation; ultimate tensile strength; pearlite; pearlitic steel; temperature; steelmaking; anneal; brittleness; brittle; metallography; metallograph; martensitic steel; quenching; water-quench; crystallite; grain structure; smectic-phase; liquid crystal; Physical Review Letters; physicist; Cornell University (Ithaca, New York); microstructure; geometry; geometrical; ellipse; hyperbola; nature; three-dimensional space; conic section; boundary value problem; boundary condition; mathematics; special relativity; Lorentz transformation; James Sethna; computer simulation; computer model; research; graphics processing unit (GPU); integrated circuit; computer graphics; video game; cluster analysis; clustering algorithm; puzzle; aesthetics; Euclidean geometry; abstract art; century; French; Georges Friedel; molecule; sphere; Dupin cyclide; cyclides of Dupin; point reflection; inversion; torus; computer graphics; computer; chip; U.S. Department of Energy; Simons Foundation.