Resistor Networks
September 26, 2016
While most
audio signal processing is now done using
digital circuitry, it's often easier in some cases to implement simple
audio filters using venerable
analog circuit techniques. While using an analog
bandpass filter in a recent circuit design, I ran into the common problem of needing an uncommon
resistance value to hit the desired
frequency.
I did what most
electrical engineers do in that case, I used a
parallel combination of two
resistors. The problem could have been solved, also, by a
series combination of two resistors. In my case, a parallel combination of a 470
k-ohm and a 1
meg-ohm resistor gave a resistance of 320 k-ohms, close enough to my desired 330 k-ohms. The
formulas for
calculating series and parallel resistance are found in the figure, below.
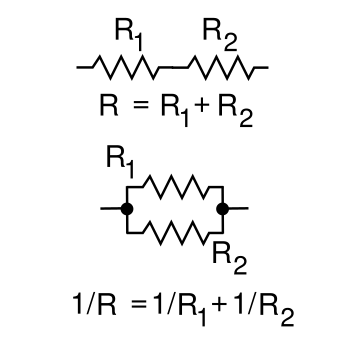
Resistors in series and parallel combination.
In the series case, the resistance R is calculated as the sum of the individual resistances. In a parallel combination, the conductance, which is the reciprocal of the resistance, is summed.
(Created using Inkscape.)
It's easy to validate these formulas by looking at how resistance arises at the
physical level. The resistance
R of a regularly shaped piece of a
material with resistivity ρ, cross-sectional area A and
length L, as shown in the figure, is just
R = ρ (L/A).
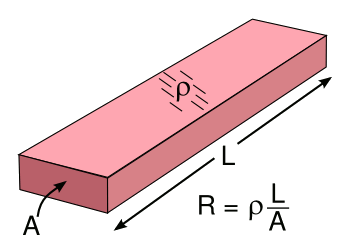
Resistance formula for a conductor with resistivity, ρ.
(Illustration by the author using Inkscape.)
When we put resistors in series, we're adding the lengths of their internal conductors, so the simple addition suffices. When we put resistors in parallel, we're adding the cross-sectional areas.
Inverting the resistance formula allows an addition of the areas. These concepts of series and parallel resistance can take us quite far in the
analysis of resistor networks, as shown in the two different connections of resistors between three
terminals, as shown in the figure.
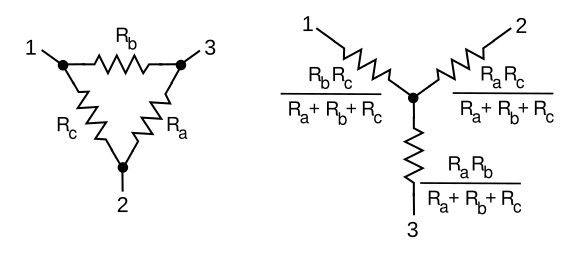
Y-Delta resistor networks and their equivalent resistor values. (Created using Inkscape.)
The
transformation of values in these two networks was first published by
Arthur Edwin Kennelly in 1899.[1] Kennelly was the
thesis advisor of
Vannevar Bush at
MIT. It's easy to see how the resistance between
nodes in the delta configuration (left) can be calculated as a parallel combination of a resistor and two series resistors. In the Y configuration (right), a series combination is all that's needed. Some lengthy, but not too advanced,
algebra is all that's needed to find which values of resistors will give the equivalent resistance between the nodes.
Since I'm an
experimentalist at heart, I decided to test these
equations, first connecting nominal 1 k-ohm, 2.2 k-ohm, and 4.7 k-ohm resistors in the Δ-configuration. The measured values of these resistors, and the calculated resistors for the Y-configuration are listed below (values in ohms).
| RA = 996 | | R1 = 1315 |
| RB = 2202 | | R2 = 595 |
| RC = 4740 | | R3 = 276 |
I used
variable resistors to create the values needed for the Y-configuration. The
measured resistance values between nodes match quite well, as can be seen in the table. Any
errors likely arise from my
instrumentation, a hand-held
digital volt-ohm-milliamp meter.
| Nodes | Resistance
(calc) | Δ
(meas) | Y
(meas) | Error
Δ (%) | Error
Y (%) |
| 1-2 | 1909.6 | 1909 | 1902 | 0.0 | -0.4 |
| 2-3 | 871.0 | 871 | 873 | 0.0 | 0.2 |
| 3-1 | 1591.2 | 1540 | 1590 | -3.2 | -0.1 |
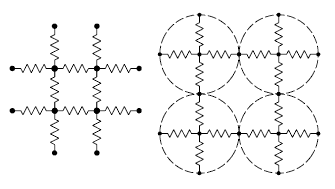
These preliminaries lead us to what I think is the most interesting network of resistors; that is, the
infinite lattice of resistors shown in the figure. Adding a touch of infinity to a problem makes it both more interesting and often more complex.
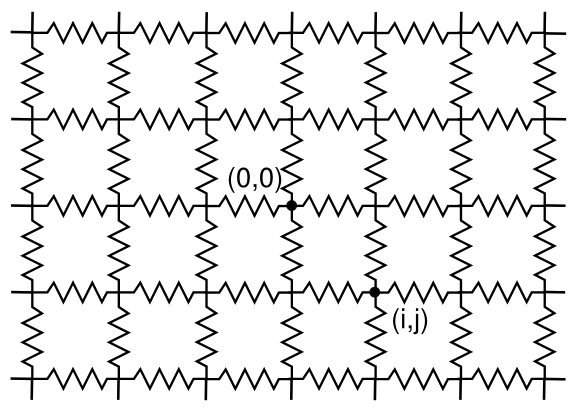
An infinite lattice of resistors in two dimensions, connected at each crossing. The resistance between some of the nodes will give an experimental value of pi (π). (Illustration by the author using Inkscape.)
A very nice analysis of this infinite array of resistors was
published in 1999,[2] and there have been many papers on this lattice array, similar lattice arrays, and cubic arrays, published on
arXiv.[2-11] The following table shows the calculated resistance values, in units of the identical resistance values in the array, between the
origin (0,0) and some nearby lattice nodes.[2] Since this is an infinite array, the origin can be anywhere.
| (i,j) | R | |
(i,j) | R |
| 0,0 | 0 | || |
2,2 | (8/3π) |
| 0,1 | 1/2 | || |
3,3 | (46/15π) |
| 1,0 | 1/2 | || |
4,4 | (352/105π) |
| 1,1 | 2/π | || |
5,5 | (1126/315π) |
It's interesting that the resistance between some nodes will give
rational numbers, while other nodes will give values containing π, an irrational, transcendental number.
Infinite resistor networks of this sort are useful for modeling the conductivity of assemblages of discrete conductors. As shown in the figure, the conductivity of particle assemblages can be modeled by their internal resistance, and the resistive links to
nearest neighbors. While the figure shows the two-dimensional case, there can be
three-dimensional arrays.
Electrical percolation can be modeled this way.
Modeling electrical conductivity in a rectangular array of particles.
The model has resistive links to nearest neighbors.
Fig. 1 of ref. 12, via arXiv
References:
- A.E. Kennelly, "Equivalence of triangles and three-pointed stars in conducting networks", Electrical World and Engineer, vol. 34 (1899), pp. 413-414. An early tutorial can be found at Robert D. Evans, "Analytical Solutions," The Electrical Journal, vol. XVI, January-December, 1919, pp. 345-349 (via Google Books).
- D. Atkinson and F. J. van Steenwijk, "Infinite resistive lattices," Amer. Jour. Phys., vol. 67, no. 6 (June, 1999), pp. 486-492. A PDF copy can be found, here.
- N.Sh. Izmailian, and R. Kenna, "A generalised formulation of the Laplacian approach to resistor networks," arXiv, June 19, 2014.
- M. Owaidat, "On the uniform tiling with electrical resistors," arXiv, May 25, 2013.
- J. H. Asad, "Infinite Body Centered Cubic Network of Identical Resistors," Arxi, February 19, 2013.
- Jihad H. Asad, "Exact Evaluation of The Resistance in an Infinite Face-Centered Cubic Network," Arxiv, October 7, 2012.
- J. H. Asad, "Infinite Face Centered Cubic Network of Identical Resistors," Arxiv, May 5, 2012.
- Jozsef Cserti, Gabor Szechenyi and Gyula David, "Uniform tiling with electrical resistors," Arxiv, March 7, 2011.
- J. H. Asad, R. S. Hijjawi, A. J. Sakaji and J. M. Khalifeh, "Resistance Calculation for an infinite Simple Cubic Lattice- Application of Green's Function,", May 1,2009.
- J. H. Asad, A. J. Sakaji, R. S. Hijjawi and J. M. Khalifeh, "On the resistance of an Infinite Square Network of Identical Resistors- Theoretical and Experimental Comparison," arXiv, April 3, 2009.
- R. S. Hijjawi, J. H. Asad, A. J. Sakaji, M. Al-Sabayleh and J. M. Khalifeh, "Infinite Simple 3D Cubic Lattice of Identical Resistors (Two Missing Bonds)," arXiv, March 24, 2009.
- Yakov M. Strelniker, Shlomo Havlin, Richard Berkovits, and Aviad Frydman, "Resistance distribution in the hopping percolation model," arXiv, June 7, 2005.
- Thomas Lam, "Electrical Resistor Networks," Notices of the American Mathematical Society, vol. 63, no. 8 (September, 2016), pp. 875f., DOI: http://dx.doi.org/10.1090/noti1420 (PDF file).
Permanent Link to this article
Linked Keywords: Audio signal processing; digital; electronic circuit; circuitry; audio filter; analog electronics; analog circuit; bandpass filter; resistance; frequency; electrical engineering; electrical engineer; parallel combination; resistor; series combination; ohm; k-ohm; meg-ohm; formula; calculation; conductance; multiplicative inverse; reciprocal; Inkscape; physics; physical; material; resistivity; cross-sectional area; length; inverting; network analysis; analysis of resistor networks; terminal; Y-Delta transform; transformation; Arthur Edwin Kennelly; doctoral advisor; thesis advisor; Vannevar Bush; Massachusetts Institute of Technology; MIT; node; algebra; experimentalist; equation; potentiometer; variable resistor; measurement; measure; errors and residuals in statistics; instrumentation; multimeter; digital volt-ohm-milliamp meter; infinity; infinite; lattice graph; square grid graph; two-dimensional space; experiment; experimental; pi; analysis; scientific literature; publish; arXiv; origin; rational number; irrational number; transcendental number; computer simulation; modeling; Voronoi diagram; nearest neighbor; three-dimensional space; electrical percolation.