Prime Number Cousins
April 14, 2016
Prime numbers are those natural number greater than one that have no positive divisors except themselves and one. All the other natural numbers are composite numbers, which are numbers constructed by multiplying prime numbers together. While it seems to be in strange company with all those odd numbers, the number two is prime, since that's the only way we can construct the even numbers.
A theorem with the impressive title, the fundamental theorem of arithmetic, asserts that any natural number greater than one can be expressed as a product of primes in just one way. As an example, the
taxicab number,
1729, is
7 x 13 x 19, and it can't be expressed by any other combination of primes.
One
illustration I remember from
Irving Adler's Giant Golden Book of Mathematics[1] was the sieve of Eratosthenes This illustration by Lowell Hess, who illustrated quite a few children's books in his
career, depicted an actual
mechanism for filtering numbered
cubes to find the prime numbers. The following figure illustrates such a mechanism.
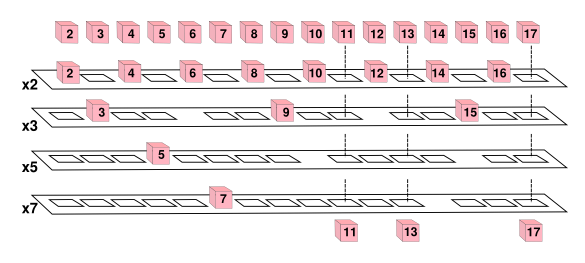
The sieve of Eratosthenes, illustrated as a physical mechanism. The first platform has holes cut to stop all numbers divisible by two, and pass all others. The second platform catches all numbers divisible by three, etc. The prime numbers are the first number stopped on each level. Since the first platform catches all even numbers, platforms to stop numbers divisible by four, six, and all other even numbers, are not included. (Illustration by the author using Inkscape.)
Since prime numbers are such an important part of number theory,
mathematicians have long searched for regularities in their
enumeration. I wrote about two of these in previous articles (
Prime Gap, January 15, 2015 and
The Twin Prime Conjecture, June 3, 2013). The most important such regularity is the
prime number theorem, which encapsulates the idea that large prime numbers are rare. It states that the
probability that a number
N is prime is
1/(ln(N)), where ln(N) is the
natural logarithm of N.
Scientists, and
mathematicians who work in the
sciences, often find themselves at
scientific conferences, suffering through one
boring talk or another while waiting for the speaker that they're really interested in hearing. Mathematician,
Stanislaw Ulam found himself at one such meeting in 1963, at which he
doodled a
spiral of numbers and found that prime numbers were more likely found on some
diagonal lines in this spiral, now called the
Ulam spiral (see figure).
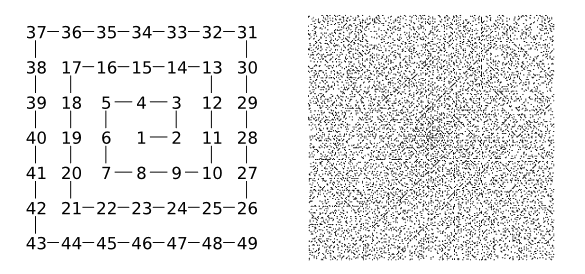
Left, construction of Ulam's number spiral. Right, the primes in the first 100,000 numbers plotted on the Ulam number spiral. (left image, modified, and right image, by Luciano Che, from Wikimedia Commons.)
The consequence of this tendency of the primes to fall on select diagonals is that a number
n is more likely to be prime if it's a solution of the
equation,
f(n) = 4n2 + bn + c
where
b and
c are
constants.
Another unusual property of prime numbers has been discovered by two mathematicians from
Stanford University (Stanford, California).
Robert Lemke Oliver and
Kannan Soundararajan have discovered that a prime number ending in
9 is about 65% more likely to be followed by a prime number ending in
1 than another prime number ending in
9.[2-3] They present both their
empirical evidence and a
theoretical reason for this property in a recent
arXiv posting.[2]
Evidence has been presented before for such strange
correlations. In a 2011 paper, a team of mathematicians from
Boston College and
Ohio State University followed up on a
conjecture, called the
prime k-tuples conjecture, by the famous number theory pair,
Hardy and
Littlewood. They used a
computer to amass evidence that prime pairs of the form
(p, p+n) occur often. They found that prime pairs of the form
(p, p+6) occur twice as often as
twin primes, but this is still quite rare.[4-5] The prime k-tuples conjecture, which is unproven but supported by a lot of empirical evidence, gives estimates of occurrence of primes at all given spacings.[3]

Mathematician, Godfrey Harold Hardy (1877-1947) is known, also, for being the mentor of number theory marvel, Srinivasa Ramanujan.
Hardy wrote in his Mathematician's Apology, that "No discovery of mine has made, or is likely to make, directly or indirectly, for good or ill, the least difference to the amenity of the world."
(Via Wikimedia Commons.)
It's reported that Oliver and Soundararajan's result is the "exact opposite of what most mathematicians would have predicted," since it's believed that prime numbers behave like
random numbers.[3] If they did behave like random numbers, then a prime ending in one digit should be followed by any another digit in equal probability, shouldn't it?[3] Oliver and Soundararajan write that it's important to understand your
randomness before questioning it.[3]
Using the prime standard of randomness, the flip of a
fair coin, they offer the following example. If
Kirk flips a coin until he sees a head followed by a tail, while
Spock flips a coin until he sees two heads in a row, in the long run, Kirk will need four flips to get his result, while Spock will require six flips.[3] I verified this using a
computer simulation (
source code here). For 100,000 trials, I get 4.005680 and 6.002250.
Soundararajan and Oliver first examined first 400 billion primes in
base-3, and they found that primes with the same last digit seemed to avoid appearing in succession.[3] They found that this property was true in
base-10, also, as well as all other
bases tested.[3] One plausible reason for this, which relates to the coin-flip example, above, is that the prime number pair
(p, p+10) in base-10 would have a good chance of having a prime
(p+2),
(p+4),
(p+6), or
(p+8), appear between them. The actual reason is a little deeper than this, since the biases they uncovered are greater than what this simple model would predict.[3]
It's uncertain whether this new property of prime numbers is important to deeper questions about the primes, but it's interesting that such a simple fact lay undiscovered all this time; and, it was a discovery generated by
experimental mathematics; i.e., computer mathematics.
References:
- Irving Adler (Author), Lowell Hess (Illustrator), "The Giant Golden Book of Mathematics," Golden Press, first edition 1958, 92 pp. (via Amazon).
- Robert J. Lemke Oliver and Kannan Soundararajan, "Unexpected biases in the distribution of consecutive primes," arXiv, March 11, 2016.
- Erica Klarreich, "Mathematicians Discover Prime Conspiracy," Quanta Magazine, March 13, 2016.
- Avner Ash, Laura Beltis, Robert Gross, and Warren Sinnott, "Frequencies of Successive Pairs of Prime Residues," Experimental Mathematics, vol. 20, no. 4(November 28, 2011), pp. 400-411. A PDF file is available here.
- G.H. Hardy and J.E. Littlewood, "Some problems of Partitio Numerorum III: On the expression of a number as a sum of primes," Acta Mathematica, vol. 44, no. 1 (December, 1923), pp. 1-70.
Permanent Link to this article
Linked Keywords: Prime number; natural number; positive; divisor; composite number; multiplication; multiply; even number; theorem; fundamental theorem of arithmetic; product; taxicab number; 1729; illustration; Irving Adler; sieve of Eratosthenes; children's literature; children's book; career; mechanism; cube; physics; physical; Inkscape; number theory; mathematician; enumeration; prime number theorem; probability; natural logarithm; scientist; science; academic conference; scientific conference; boredom; boring; Stanislaw Ulam; doodle; spiral; diagonal line; Ulam spiral; Wikimedia Commons; equation; constant; Stanford University (Stanford, California); Robert Lemke Oliver; Kannan Soundararajan; empirical evidence; theory; theoretical; arXiv; correlation; Boston College; Ohio State University; conjecture; prime k-tuples conjecture; G. H. Hardy; John Edensor Littlewood; computer; twin prime; mentor; intellectual giftedness; marvel; Srinivasa Ramanujan; Mathematician's Apology; randomness; random number; fair coin; James T. Kirk; Spock; computer simulation; source code; coin flip.c; ternary numeral system; base-3; decimal; base-10; radix; base; experimental mathematics; Irving Adler (Author), Lowell Hess (Illustrator), "The Giant Golden Book of Mathematics," Golden Press, first edition 1958, 92 pp.