Circumscribing Semicircles with Triangles
August 15, 2016
Humans are fascinated by
circles, so much so that many objects are circular in shape, many expressions contain the word, circle, and many
English words begin with the
prefix, "circum-," derived from the
Latin word for circle. One massive
online word list has more than 250 words starting with circum, including
circumlocution,
circumspect,
circumstantial, and
circumvent.

Both sides of a replica of the 3,500 year old Phaistos Disk, a fired clay disk about six inches in diameter. The disk is covered on each side with stamped symbols of an unknown language similar to Linear A and Linear B. (Photo by Maksim, via Wikimedia Commons.)
Geometerss are well acquainted with circles, and also
polygons inscribed within, and
circumscribed around, circles. At about 250
BC, the
Greek mathematician,
Archimedes, circumscribed a
hexagon and polygons up to 96 sides around a circle to get
good estimates of the
mathematical constant,
pi.
A side of a hexagon circumscribed around a circle of unit
diameter is 1/√3, so that its
perimeter is 6/√3, or 3.46. A hexagon inscribed in a circle has a perimeter of 3.0 (see figure). The value of pi, Archimedes reasoned, was in between these values. The value found for a circumscribed 96-sided polygon is 22/7, the
elementary school approximation of pi (3.1429).
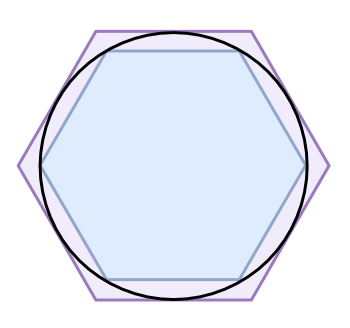
Hexagons inscribed within, and circumscribed around, a circle.
The circumscribed hexagon gives an approximate value for pi of 3.46, while the inscribed hexagon gives 3.0. The actual value of pi (3.1415926535...) is between these estimates.
(Via Wikimedia Commons.)
I find
plane geometry problems enjoyable, since they are quite simply stated. Some of them are also amenable to a
computer solution, so they allow me to practice my (limited)
computer programming skill.
In a recent
arXiv posting, Jun Li of the
Jiangxi University of Science and Technology (Ganzhou, China) presented the problem of finding the
triangle of smallest
area that can be circumscribed around a
semicircle.[1] He did an
analytical solution of the problem under a particular
constraint, but his
paper got me interested in the general problem.
As can be seen in the figure, triangles circumscribed around a semicircle come in many sizes. You can circumscribe
right triangles, fat triangles, and tall triangles. The constraint in this case is that the base of the triangle aligns with the
base of the semicircle, and the two other sides are
tangent to the
curve of the semicircle.
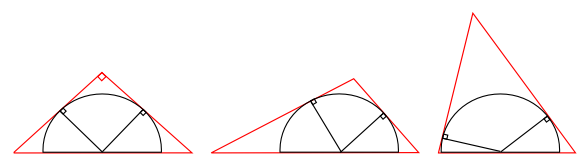
A variety of triangles circumscribed about a semicircle. (Illustration by the author using Inkscape.)
In searching for the circumscribed triangle of minimum area, I found that it was easiest to specify the
angles of the
altitudes from the base of the unit semicircle, as shown in the figure. It was then time to extract the long dormant
information I had learned in my
high school geometry class. As an indication of how long ago that was, I attended my 50th high school
reunion last year.
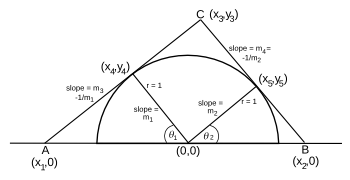
(Illustration by the author using Inkscape. Click for larger image.)
Some important ideas of this computation are that the
slopes of
perpendicular lines are their
negative reciprocals, and
intersecting points (x,y) are found by
equating the line
equations,
y = mx + b, where
m is the slope and
b is the
y-intercept. The
sine and
cosine functions are useful for finding the length of the sides of right triangles when an angle and the length of another side are known.
In the past, a computer program of this sort would use a
minimum value search
algorithm akin to the
method of steepest descent. Today's computers are so fast that a
lazy programmer can do an
exhaustive search in a problem like this, perhaps with a reduction in the
variable increments as they get close to the goal; or, the
Monte Carlo method that I used, in which you try
random values and keep track of how well you're doing. My
C language source code, in my usual
amateur coding style, can be found
here
So what's the result? A proper
mathematician might have told me that it was obvious that an
isosceles right triangle (θ
1 = θ
2 = 45°) gives the minimum area. For a semicircle radius of one, the area is 2.0. This can be seen from the
contour plot, shown below, that also indicates how slowly the area changes with angle.
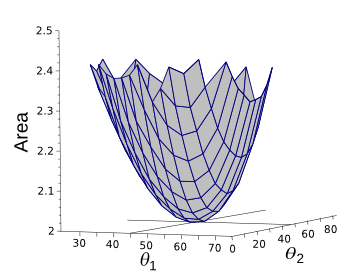
Contour plot of triangle areas.
(Created from data from the author's program using Gnumeric.)
![]()
Reference:
- Jun Li, "The Triangle of Smallest Area Which Circumscribes a Semicircle," arXiv, June 27, 2016.
Permanent Link to this article
Linked Keywords: Human; circle; English language; prefix; Latin; Internet; online; circumlocution; circumspect; circumstantial; circumvent; replica; Phaistos Disk; furnace; fire; clay; inch; diameter; stamping; stamped; symbol; Linear A; Linear B; Wikimedia Commons; Euclidean geometry; geometer; polygon; inscribed figure; tangential polygon; circumscribe; Anno Domini; BC; Ancient Greece; Greek; mathematician; Archimedes; hexagon; polygon approximation; estimate; mathematical constant; pi; diameter; perimeter; elementary school; approximation; plane geometry; computer; computer programming; arXiv; Jiangxi University of Science and Technology (Ganzhou, China); triangle; area; semicircle; mathematical analysis; constraint; academic publishing; paper; right triangle; base; tangent; curve; Inkscape; angle; height; altitude; information; high school; class reunion; slope; perpendicular; line segment; negative number; multiplicative inverse; reciprocal; intersection; intersecting; point; equating; equation; y-intercept; sine; cosine; trigonometric function; minimum value; algorithm; method of steepest descent; sloth; lazy; programmer; brute-force search; exhaustive search; independent variable; increment; Monte Carlo method; randomness; random value; C programming language; source code; amateur; circumscribe.c; mathematician; isosceles triangle; contour plot; Gnumeric.