Ballistics
December 19, 2016
Digital computers were not the first
electronic computers. There was a span of several
decades in which
analog computers were used to solve come common problems. It's fairly easy to implement the
mathematical functions of
integration and
differentiation using
operational amplifiers, the earliest of which were built using
vacuum tubes. Notable
electrical engineer,
Robert Pease (1940-2011), who designed some early operational amplifiers while at
George A. Philbrick Researches,[1] has written many articles about their history and design.[2-4]

An operational amplifier integrator.
In operation, the capacitor is discharged to make the output voltage zero at time zero. Having the same value resistor in the non-inverting input eliminates drifting caused by input bias currents.
(Created using Inkscape.)
Since I'm a member of the
baby boomer generation, my
physics education included
laboratory exercises in
analog computation. The one exercise that I remember most is
calculating the
trajectory of a
projectile, the results of the calculation being displayed on an
x-y chart recorder. The interesting part of that exercise was seeing the difference in trajectory between a projectile launched on
Jupiter as compared with
Earth.
The trajectory of a projectile, idealized without
atmospheric drag,
Coriolis force, etc., has been known since the time of
Galileo, and it is derived by a simple addition of the motion arising from the projectile
velocity and that of the fall of the projectile arising from
gravity,
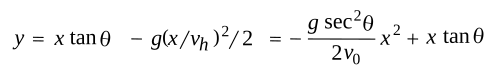
where (x,y) are the points that define the trajectory, θ is the launch
angle from the
horizontal, v
0 is the initial projectile velocity, v
h is the horizontal component (x component) of the projectile velocity (v
h = v
0 cos θ), and g is the
gravitational acceleration, 9.80665 m/sec
2. An example trajectory, as generated by a simple
C language program (
source code here), is shown below,
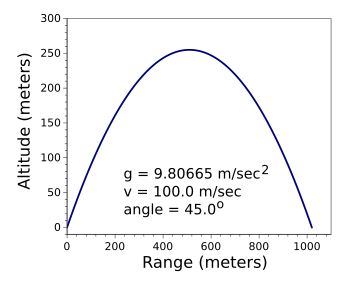
An ideal trajectory without air drag and other confounding influences.
Maximum range is achieved when the projectile is launched at 45 degrees.
(Graphed using Gnumeric.)
Isaac Newton used
ballistics to elucidate the idea of an
orbit of one body around another, such as the
Moon's orbiting the Earth. In his 1728 book, "
A Treatise of the System of the World," Newton imagined the
thought experiment, illustrated below, in which you
fired cannonballs at increasing velocities, finally reaching a point at which they fly into orbit around the Earth.[6] He then generalized this to the Moon's motion around the Earth.

Newton's own illustration of his cannonball experiment. (From Isaac Newton, "A Treatise of the System of the World," F. Fayram, 1728.[6]
The range
R of an ideal projectile is given as
R = (v2/g)sin(2θ), so you can hit a target at any range up to a maximum determined by the projectile's initial velocity
v by just setting the angle. It can be seen by inspection that the maximum range always occurs at an angle of 45 degrees, since the
sine of 90° is one. That angle, however, is not the angle at which the
length of the path of projectile travel is maximum.
It's easy to calculate the path length of a projectile as a function of angle. You just use the trajectory example presented above and do a
piece-wise integration of the path length. My source code for such a calculation can be found
here,[6] and the results of this calculation are shown below with the maximum occurring at an angle near 1
radian (57.2958°).
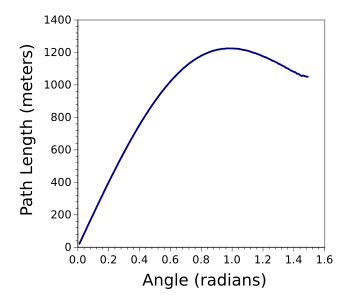
Trajectory path length as a function of launch angle.
(Graphed using Gnumeric.)
Joshua Cooper and
Anton Swifton of the
Department of Mathematics of the
University of South Carolina have
published a paper on
arXiv in which they derive an
equation to give the angle that produces the maximum projectile path length.[7] This angle, which is
independent of the initial
speed of the projectile and the value of the gravitational acceleration, is the solution of this interesting equation,
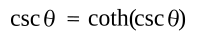
The easiest way to find the solution to an equation such as this is to use one of the many
free and open source software computer algebra systems. Cooper and Swifton used
SageMath to obtain an angle of about 0.9855 radians (56.47 degrees). I used my favorite method of refined increments (source code
here) to obtain the value 0.985514738.
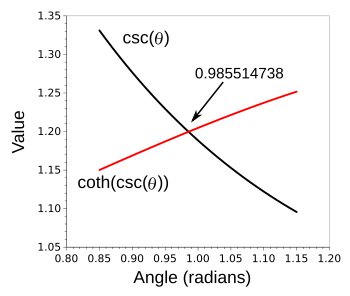
Intersecting curves, csc(θ) and coth(csc(θ)).
(Graphed using Gnumeric.)
![]()
References:
- GAP/R, George A. Philbrick Researches Archive.
- Application Brief R1, "Practical closed-loop stabilization of solid state operational amplifiers," Philbrick Archive, February 1, 1961.
- Bob Pease, "What's All This Transimpedance Amplifier Stuff, Anyhow? (Part 1)" Electronic Design, January 8, 2001.
- Bob Pease, "What's All This Julie Stuff, Anyhow?" Electronic Design, May 3, 1999.
- Isaac Newton, "A Treatise of the System of the World," F. Fayram, 1728, pp. 5-6.
- Thanks to Anton Swifton, who discovered an error in my original program.
- Joshua Cooper and Anton Swifton, "Throwing a Ball as Far as Possible, Revisited," arXiv, November 8, 2016.
Permanent Link to this article
Linked Keywords: Digital; computer; electronic; decade; analog computer; mathematical function; integral; integration; derivative; differentiation; operational amplifier; vacuum tube; electrical engineering; electrical engineer; Robert Pease (1940-2011); George A. Philbrick Researches; operational amplifier integrator; capacitor; discharge; voltage; resistor; non-inverting input; input bias current; Inkscape; baby boomer generation; physics; education; laboratory; analog computer; analog computation; calculation; calculating; trajectory; projectile; x-y chart recorder; Jupiter; Earth; atmospheric drag; Coriolis force; Galileo Galilei; velocity; gravitation; gravity; angle; horizontal plane; gravitational acceleration; C programming language; computer program; source code; trajectory.c; range; Gnumeric; Isaac Newton; ballistics; orbit; orbit of the Moon; Philosophiae Naturalis Principia Mathematica; A Treatise of the System of the World; thought experiment; Newton's cannonball; cannonball experiment; sine; length; arc length; iece-wise integration; radian; Joshua Cooper; Anton Swifton; Department of Mathematics; University of South Carolina; scientific literature; publish; arXiv; equation; independent variable; speed; free and open source software; computer algebra system; SageMath; solver.c; trigonometric function; csc; hyperbolic function; coth.