Avoided Numbers
May 12, 2016
New York State initiated its
sales tax on April 14, 1965, while I was there attending
high school. At its initiation, this tax was just 2%, but it quickly ramped up over the years, with
counties adding their own sales taxes. Fortunately, many items are excluded from sales tax, including
funeral expenses. In a small sense,
you can take it with you.
When this sales tax was initiated, I realized that it would be impossible to buy some items at certain
prices. As an example, consider the
sales tax for New Jersey, presently at 7%.[1] There is no sales tax on an item costing ten
cents, but there's a one cent sales tax on an item costing eleven cents. That means that you can't pay eleven cents for an item. You can only buy that item for twelve cents. Eleven is a
forbidden number.
Because of this sales tax, it's impossible to buy items for 11, 21, 35, 51, 67, 83, or 97 cents. As the following
graph shows, there are seven forbidden prices in each
dollar interval.
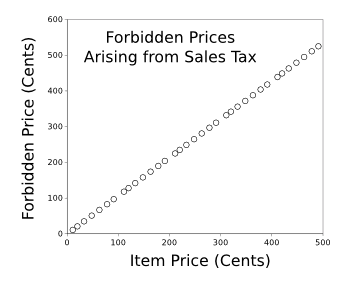
Forbidden prices for goods in New Jersey as a consequence of its 7% sales tax.
(Graphed using Gnumeric.)
While
seven is considered to be a
lucky number by some people, it was a number to be avoided in certain
cultures under certain circumstances. When doubly
cursed by seven, as being the
seventh son of a seventh son, you might be a
vampire. Fortunately,
science has dispelled such
numerology, although
some physicists think that
it still persists in
string theory.[2]
Consider a person who's so afraid of the number, seven, that he refuses to leave his
house on the seventh day of each
month. Moreover, he chooses to remain inside on the 17th and 27th of each month. A little strange, but he could still function in the
modern world by making up lost
work days on
weekends.
Then comes the month of
July, the seventh month. He would need to stock a lot of
food, and take that month as his work
vacation. He's still able to function in our modern world. His big problem arises next year,
2017. While we leave our subject's
researching use of the
Hebrew calendar and other
calendars as a possible remedy, it's interesting to consider how many numbers we would need to reject from the
natural numbers if we wished to avoid a particular
digit.
Often it's easier to
calculate something in the
converse, so we'll calculate the
probability that a number
does not contain a particular digit. For numbers from 0-9, this would be 9/10. For a two digit number, we need to
multiply this probability to get (81/100), which means we should expect 19 numbers in that range to contain a seven, which is
verified by inspection. As the following graph shows, it becomes more difficult to find a number devoid of the digit, seven, as we go to larger numbers.

Probability that a number will not contain a particular digit (for example, seven) as a function of the number of its digits.
(Graphed using Gnumeric.)
This result is simply expressed as
p(n) = (9/10)n, where
n is the number of digits of the number, and it can be expressed in an arbitrary
base b as
p(n) = (b-1/b)n. Obviously, the curve for
hexadecimal numbers (base-16) will descend less quickly, and
octal numbers (base-8) will have a steeper
curve, as shown below.
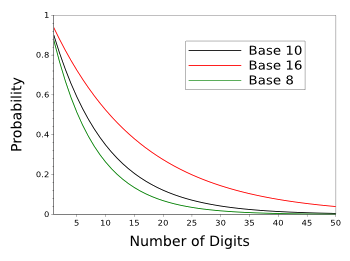
Avoided digit probability for base-16, base-10, and base-8.
(Graphed using Gnumeric.)
To find how many numbers fulfill our avoided-digit
criterion up to a number
N, we need to
integrate under these curves. Lazy
mathematician that I am, I resort to the result given in a recent
arXiv paper by
James Maynard.[3]
The numbers fulfilling the avoided-digit criterion up to
N are of the order,
O(N(1-c)), where
c = log(b/(b-1))/log(b). For decimal numbers,
c ≈ 0.045757. Although the probability is low, up to 100 decimal digits we still obtain 2.65 x 10
95 numbers meeting our avoided digit criterion.
In his arXiv paper, Maynard addressed the question of whether there are an
infinity of
prime numbers in the
set of such avoided-digit numbers. The infinity of primes among all the natural numbers was
established by Euclid in his
Elements, Book IX, Proposition 20, a
proof that's easy enough for a high school student to understand.

So, you thought that your math books were difficult to read.
Proposition 5 from book II of Euclid's Elements in the Oxyrhynchus papyrus, I-29.
(Via Wikimedia Commons.)
While the details of Maynard's proof in his 44 page paper are beyond my grasp, he apparently was able to show that there are infinitely many prime numbers which do not have a particular digit in their decimal expansion.[3]
References:
- Sales Tax Collection Schedule, State of New Jersey, Department of the Treasury, Division of Taxation, July 15, 2006 (PDF file).
- Lee Smolin, "The Trouble With Physics: The Rise of String Theory, The Fall of a Science, and What Comes Next," Mariner Books, September 4, 2007, 416 pp, ISBN: 978-0618918683.
- James Maynard, "Primes with restricted digits," arXiv, April 4, 2016.
Permanent Link to this article
Linked Keywords: New York State; sales tax; high school; county; funeral; You Can't Take It with You; you can take it with you; price; sales tax for New Jersey; cent; forbidden; number; Cartesian coordinate system; graph; dolla; Gnumeric; seven; luck; lucky; culture; curse; seventh son of a seventh son; vampire; science; numerology; Lee Smolin; physicist; The Trouble with Physics; string theory; house; month; contemporary history; modern world; workweek and weekend; work day; weekend; July; food; vacation; 2017; research; Hebrew calendar; calendar; natural number; numerical digit; calculation; calculate; converse; probability; multiplication; multiply; verified by inspection; probability; Gnumeric; radix; base; hexadecimal; octal; curve; base-16; base-10; base-8; criterion; integral; integrate; mathematician; arXiv; James Maynard; infinite set; infinity; prime number; set; Euclid's theorem; Euclid's Elements; mathematical proof; Oxyrhynchus papyrus, I-29; Wikimedia Commons; Lee Smolin, "The Trouble With Physics: The Rise of String Theory, The Fall of a Science, and What Comes Next," Mariner Books, September 4, 2007, 416 pp, ISBN: 978-0618918683.