| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Numerology
March 2, 2015
The
Greek philosopher,
Pythagoras, is known to everyone for the
Pythagorean theorem, but his greatest impact in his own time was as founder of the
religious movement,
Pythagoreanism. Little is known about this
pre-Socratic philosopher, but it's thought that disciples of Pythagoreanism believed that
numbers were the ultimate
reality. This idea that reality is different from what we observe is a feature, also, of the philosophy of
Plato, and it's conjectured that Plato was influenced by Pythagoras.
Pythagoras (Πυθαγορας)
c. 570 - c. 495.
(From Mathematicians and astronomers: twenty portraits, engraving by J.W. Cook, 1825, via Wikimedia Commons.)
Pythagoras had the idea that 10 was the most perfect number, possibly through examination of his
fingers and
toes.
Mathematicians have their own
perfect numbers, which are numbers whose value equals that of all their
divisors excluding themselves. Thus, ten is not a perfect number in today's sense, since 1 + 2 + 5 ≠ 10, but six is (1 + 2 + 3 = 6). Whether or not there are an
infinity of perfect numbers is an
unsolved problem in number theory.
The Pythagoreans represented the perfection of ten by a graphic, called the
tetractys (τετρακτυς), as shown below.
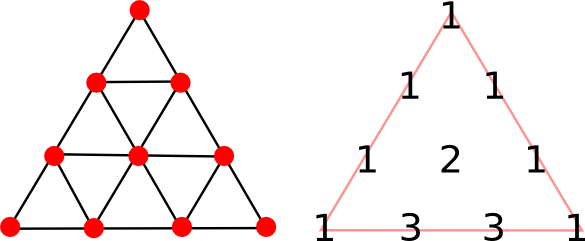
The tetractys (left) and the top of Pascal's triangle (right). (Illustration by the author, rendered using Inkscape.)
There was a lot of
symbolism in the tetractys aside from the number of points adding to ten. The last row of four relates to the
four classical elements,
Earth,
Air,
Fire and
Water.
As you can see from the figure, the tetractys acts as a
template for the
coefficients of the
polynomial expansion of (x + 1)
n; for example, the last row represents (x + 1)
3 = 1x
3 + 3x
2 + 3x
1 + 1x
0. This
triangular array of coefficients is known as
Pascal's triangle, named after the
French mathematician,
Blaise Pascal. The coefficients are series
A007318 in the
On-Line Encyclopedia of Integer Sequences. I wrote about Pascal in a
previous article (Blaise Pascal, June 19, 2012).
Physics is typically the realm of numbers with
dimensions that are mixtures of
powers of
length,
mass,
time, and sometimes
charge. That's why the predominant system of measurement before the
International System of Units was "
MKS," for meter-kilogram-second. However, it's possible to arrange
fundamental physical constants to yield
dimensionless numbers. One example of this is the fine structure constant, denoted by the
Greek letter,
α.
The fine structure constant is related to some rather fundamental things; namely, the
elementary charge e, Planck's constant h, the speed of light c and the mathematical constant π,
α = (2 π e2)/(h c)
This constant, which is quite close to the reciprocal of 137 (~1/137.036), expresses the strength of the
interaction of charged particles. It's fundamental to
electromagnetism, and it combines those three fundamental physical constants, e, h and c. At one time, its calculated value was very close to 1/136. Now, it's very close to 1/137.
Eminent physicist,
Arthur Eddington, thought that there was something "magical" about this number, and he proposed some
a priori reasons why it should have that value. Eddington continued to investigate dimensionless numbers, deriving an
a priori value for the number of
protons in the
universe. This number, now called the
Eddington number, is calculated to be 136 x 2
256, or 137 x 2
256, or about 10
80.
Paul Dirac made similar observations.
Physicist, Sir Arthur Stanley Eddington (1882-1944)
(United States Library of Congress, Prints and Photographs Division, image ggbain.38064, via Wikimedia Commons.)
To most physicist of the time, all this seemed to be a retreat, from the way modern physics is practiced, to the philosophy of
Aristotle. Some compared it to the ancient practice of
numerology. In fact,
Guido Beck,
Hans Bethe, and
Wolfgang Riezler published a
parody of this approach in the respected physics
journal,
Die Naturwissenschaften,[1-2] in which they related the dimensioned value of
absolute zero temperature, T
0 = -273 °C, to the fine structure constant; viz.,
T0 = -(2/α - 1)
Since many people still believe in "
lucky numbers," (not to be confused with a mathematician's
lucky numbers) it's interesting to see how words are transformed into single
digits. You can associate the digits, 0-9, with
letters of the alphabet, as shown in the table. All this is rather arbitrary, but we're not operating in the realm of
science when we do numerology.
We can then add together the numbers associated with every letter in a word. Taking
Tikalon as an example, 2 + 9 + 2 + 1 + 3 + 6 + 5 = 28. If we're interested in just a single digit, we do repeated partitions and sums to yield 2 + 8 = 10, and 1 + 0 = 1. Thus, Tikalon's "lucky number" is one. As a scientist, I'm not inclined to play 111 in the
New Jersey State Lottery; or, for that matter, play the
lottery at all.
In a recent paper on
arXiv, mathematicians
Steve Butler,
Ron Graham, and
Richard Stong examine this "partition and sum" process. They treat a more general case in which just a single plus sign is inserted into the number, or as many as one plus sign between every digit, and they consider numbers written in
binary (base-two) format. They are able to show that very few
iterations of such operations are needed to get down to the single digit, one.[3]
In examining the
bound on how many steps it takes to get a binary number down to 1, they observe that inserting as many plus signs as possible (that is, summing all the digits) for a number n results in a new number of the order
log(n). The problem then reduces to how long it takes for log(log(· · · (log(n)) · · · )) to get to a value less than one. As you can see, you might need an
infinite number of iterations, but the number of iterations grows very much more slowly than n.[3]
References:
- G. Beck, H. Bethe, and W. Riezler, "Remarks on the quantum theory of the absolute zero of temperature," Die Naturwissenschaften, vol. 2 (1931), p. 39.
- Ben Weiner, A parody paper in solid state physics, published in 1931," Tohoku University Web Site, April 25, 1997. This is an English translation of ref. 1.
- Steve Butler, Ron Graham, and Richard Stong, "Partition and sum is fast," arXiv, January 14, 2015.
Permanent Link to this article
Linked Keywords: Ancient Greek philosophy; Greek philosopher; Pythagoras; Pythagorean theorem; religious movement; Pythagoreanism; pre-Socratic philosopher; natural number; reality; Plato; Wikimedia Commons; finger; toe; mathematician; perfect number; divisor; infinity; unsolved problem in number theory; tetractys; Pascal's triangle; Inkscape; symbol; symbolism; classical elements; Earth; Air; Fire; Water; template; coefficient; polynomial expansion; triangle; triangular; Pascal's triangle; French; Blaise Pascal; A007318; On-Line Encyclopedia of Integer Sequences; physics; dimension; exponentiation; power; length; mass; time; electric charge; International System of Units; MKS system of units; fundamental physical constant; dimensionless number; fine structure constant; Greek alphabet; Greek letter; elementary charge; Planck's constant; speed of light; multiplicative inverse; reciprocal; Coulomb's law; interaction of charged particles; electromagnetism; physicist; Arthur Eddington; a priori; proton; universe; Eddington number; Paul Dirac; Dirac large numbers hypothesis; Aristotle; numerology; Guido Beck; Hans Bethe; Wolfgang Riezler; parody; scientific journal; Die Naturwissenschaften; absolute zero temperature; lucky number; numerical digit; letters of the alphabet; science; Tikalon; New Jersey State Lottery; lottery; arXiv; Steve Butler; Ron Graham; Richard Stong; binary number; iteration; bounded set; bound; natural logarithm; log(n); infinity; infinite number; G. Beck, H. Bethe, and W. Riezler, "Remarks on the quantum theory of the absolute zero of temperature," Die Naturwissenschaften, vol. 2 (1931), p. 39.