Metallophone Design
December 14, 2015
When young
children decide that their screaming doesn't make enough
noise, they find that banging on the family
pots and pans evokes louder
sounds. Eventually, they find that the sound produced by banging on a
metal railing is much more
melodious. In
my generation, long before the ubiquity of
electronics in
toys, there were
musical toys based on
mechanical impact on metal plates.
The simplest of these is the
xylophone, and this same xylophone mechanism was used to simulate a
piano. The sounds produced by these toy pianos were quite unlike the music produced by
Schroeder in the
Peanuts comic strip. Today's children are much more likely to become interested in music than children of
decades ago, since their electronic toys produce melodious tones. Why, exactly, did the toys of my childhood sound the way that they did?

Toys xylophone.
(Photo by Tomasz G. Sienicki (modified), via Wikimedia Commons.)
Mechanical impact, or stroking an edge with a
bow, will induce
vibrations in a plate. Since these vibratory
sound waves will be
reflected from the edges of the plate, they will
constructively and destructively interfere within the plate.
Ernst Chladni (1756-1827) a
German physicist and
musician known as the "father of
acoustics," did the first
research on vibrating plates.
Whether in Chladni's
18th century or today, the advancement of
science is limited by the available
instrumentation. If I were to study the vibration of plates, I would use
laser interferometry to map displacements, and
automate the
experiment using
machine vision. Chladni was able to map the
nodes of a plate, the places where displacement is very small, by stroking the edge with a bow, sprinkling
sand on the surface, and seeing where the sand persists.

Ernst Florens Friedrich Chladni (1756-1827)
There are quite a few YouTube demonstrations of Chladni patterns on vibrating plates.[1-3]
Chladni was the first to theorize that meteorites were extraterrestrial.
(An 18th century portrait, via Via Wikimedia Commons.)
The easiest type of plate to
analyze is a
circular plate, and since plates need to be somehow fixed, we can mount them to a post via a
center hole. Chladni derived the
resonant modes of such a plate in
Chladni's law. The resonant frequencies
f closely follow the
equation,
f = C (m + 2n)p
In which
m is the number of
linear modes (spokes) and
n is the number of
radial modes (circles). The
coefficient,
C, is a
function of the plate properties, and the
exponent,
p, is very nearly 2. This
law applies, also, to
deformed circular plates, such as
cymbals, and
bells.
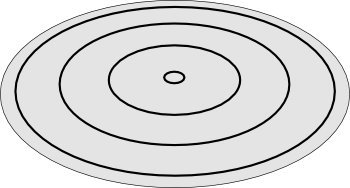
Chladni figure
Four radial modes on a center-mounted circular plate.
(Created by the author using Inkscape.)
Since radial
symmetry is not present in
square plates,
nodes in a square plate are not as simple and easy to explain as nodes in a circular plate. As can be seen in the examples below from Chladni's 1802 book,
Die Akustik, the existence of reflecting boundaries that are not equidistant from the center of the plate adds considerable
complexity to the nodes. While
calculation of the nodes is possible with
computer simulation,[4-5] an
analytical solution was difficult with the tools possessed by 18th century
mathematicians.
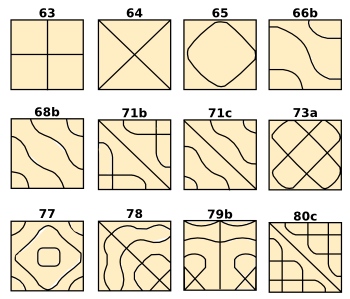
A variety of Chladni figures for a square plate from Chladni's, Die Akustik, 1802.
(Modified Wikimedia Commons image.)
The analytical solution for Chladni nodes in a square plate was
discovered after years of work by
French mathematician and physicist,
Sophie Germain (1776-1831). This solution, contained in her
paper,
Recherches sur la théorie des surfaces élastiques, was such an accomplishment that she was awarded a
prize from the
Paris Academy of Sciences. One look at her
partial differential equation will convince you that
women can do math.
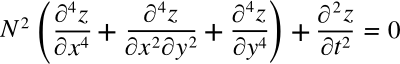
As we fast-forward to our
computer age, we can invert this problem to ask ourselves, what shape would we need to produce a specific
tone spectrum; or, how can we "tweak" an existing shape to give a better tone?
Computer scientists at
Harvard University,
Columbia University,
Disney Research, and
MIT presented work at
SIGGRAPH-Asia (Kobe, Japan) on using computational design to control the sound of an object by altering its shape.[6-7]
Their paper, "Computational Design of Metallophone Contact Sounds," tackles the particular problem of creating a toy
glockenspiel with striking elements shaped like
zoo animals (see figure).[7] Says
Gaurav Bharaj, first
author of the paper and a
graduate student at Harvard's
School of Engineering and Applied Sciences,
"Our optimization algorithm enabled us to have precise control over the sound of an object by tuning the shape of the object computationally... Through our method, we have gained control over the spectrum of frequencies and their amplitudes."[7]

A "Zoolophone" metallophone with a variety of animal shapes. The shapes were automatically created to sound with a particular tone through use of a computer algorithm. (Changxi Zheng/Columbia Engineering image.)
The toy glockenspiel is a type of musical instrument known as an
idiophone. Idiophones produce sounds in their entire structure by striking with a
mallet, so they are different from
drums, whose sound is produced just by their
membrane. Since an idiophone's sound depends on its shape, sound design for idiophones is not straightforward, and the fallback is to use simple shapes, such as bars, and to
tune these by
drilling of dimples on the underside of the bars.[7]
The "zoolophone" was a severe test of the design algorithm, since it required the striking surfaces to be in the shapes of
lions,
turtles,
elephants,
giraffes, and other animals.[7] The present algorithm is an advance over previous attempts, since it optimizes both the frequency and amplitude of the tones, including addition of
overtones that contribute to the
timbre of the
notes. Control of the timbre even allows a glockenspiel to play a chord, such as simultaneously sounding the notes
C,
E, and
G to create the
C-major triad.[7]
All this was done using a new
stochastic optimization method they call Latin Complement Sampling (LCS).[7] Says
Changxi Zheng,
assistant professor of
computer science at Columbia, and leader of the research team,
"Our discovery could lead to a wealth of possibilities that go well beyond musical instruments... Our algorithm could lead to ways to build less noisy computer fans, to erect bridges that don't amplify vibrations under stress, and to advance the construction of micro-electro-mechanical resonators whose vibration modes are of great importance."[7]
The research was supported by the
National Science Foundation,
Intel, the
Air Force Research Laboratory,
DARPA, and other sources.[7]
References:
- Physics Girl, "Singing plates - Standing Waves on Chladni plates," YouTube Video, April 28, 2014.
- Atto Gruppen, "Chladni plate experiment, round plate," YouTube Video, August 28, 2014.
- SBCCPhysics, Circular Centered Chladni Plate, YouTube Video, July 5, 2011.
- Wence Xiao, "Chladni Pattern," Basic studies in Natural Sciences, Roskilde University, May 31, 2010.
- Thomas Müller, "Numerical Chladni figures," European Journal of Physics, vol. 34, no. 4 (May 29, 2013), DOI: 10.1088/0143-0807/34/4/1067. Also at arXiv.
- Gaurav Bharaj, David I.W. Levin, James Tompkin, Yun Fei, Hanspeter Pfister, Wojciech Matusik, and Changxi Zheng, "Computational Design of Metallophone Contact Sounds," SIGGRAPH Asia 2015 (To Appear, ACM TOG, vol. 34, no. 6).
- Holly Evarts, "Change the shape, change the sound," Columbia University Press Release, November 2, 2015.
Permanent Link to this article
Linked Keywords: Child; children; noise; cookware and bakeware; pots and pans; sound; metal; handrail; railing; melody; melodious; baby boomer; my generation; electronics; toy; music; musical; mechanical impact; xylophone; >piano; Schroeder; Peanuts; comic strip; decade; xylophone; Tomasz G. Sienicki; Wikimedia Commons; bow; vibration; sound wave; reflection; reflected; interference; Ernst Chladni (1756-1827); German; physicist; musician; acoustics; research; 18th century; science; scientific instrument; instrumentation; laser; interferometry; automation; automate; experiment; machine vision; node; sand; Ernst Florens Friedrich Chladni (1756-1827); YouTube; theory; theorize; meteorite; extraterrestrial; portrait; analysis; analyze; circle; circular; center; resonance; resonant; normal mode; Chladni's law; equation; linear; radial; coefficient; function; exponent; physical law; deformed; cymbal; bell; Inkscape; symmetry; square; complexity; calculation; computer simulation; mathematical analysis; analytical; mathematician; French; Sophie Germain (1776-1831); paper; prize; Paris Academy of Sciences; partial differential equation; woman; women; information Age; computer age; spectral density; tone spectrum; computer scientist; Harvard University; Columbia University; Disney Research; Massachusetts Institute of Technology; MIT; SIGGRAPH-Asia (Kobe, Japan); glockenspiel; zoo; animal; Gaurav Bharaj; author; graduate student; School of Engineering and Applied Sciences; optimization; algorithm; amplitude; metallophone; computer algorithm; idiophone; mallet; drum; membrane; musical tuning; >drilling; lion; turtle; elephant; giraffe; overtone; timbre; musical note; C; E; G; C-major; major chord; triad; stochastic; Changxi Zheng; assistant professor; >computer science; musical instrument; computer fan; bridge; microelectromechanical systems; micro-electro-mechanical; National Science Foundation; Intel; Air Force Research Laboratory; DARPA.