The Yellowstone Sequence
February 12, 2015
People in
STEM fields learn at lot of
mathematics in their lifetime,
Counting from zero, as
computer scientists are wont to do, results in integer sequence
A001477.
The On-Line Encyclopedia of Integer Sequences (OEIS) contains more than 200,000 sequences, with about fifty new sequences being added each day. As you can imagine, it's getting harder to find a novel sequence, but this didn't deter my
colleague, Steve Sund, from finding
A181975, expressed as a(n) = abs(mod((n+3),8)-4)+1. One sequence that came to me in the
daydream state between
sleep and awakening turned out to be
A001745, the "holey numbers."
The sequence of natural numbers is fundamental, but it's also
boring. More interesting is the sequence of
prime numbers,
A000040, which has a simple rule for its construction. A prime number is a number greater than 1 with no positive
divisors except 1 and itself. A recent paper on
arXiv by several
mathematicians, including
Neil J. A. Sloane, the originator of the OEIS, concerns a sequence with a more complicated construction.
This sequence,
A098550, is called the "Yellowstone permutation," since a
graph of its elements suggests the eruption of
geysers in
Yellowstone National Park, a
park in the
U.S. state,
Wyoming. The graph has extended periods of alternating
even and
odd numbers that are interrupted by small downward spikes, followed by large upward spikes.

Old Faithful geyser in Yellowstone National Park, Wyoming
Old Faithful, as its name implies, is one of the more predictable geysers. It erupts to a height of 32-56 meters for 1.5-5 minutes in intervals of about 45 to 125 minutes.
(Photo by Kamilo Kardona, via Wikimedia Commons.)
The construction of integer sequence A098550 is as follows. Sequence elements a(n) are equal to n if n is less than or equal to 3. Otherwise, the next sequence element a(n) is the smallest number not present in the sequence up to that point having at least one common factor with a(n-2), but none with a(n-1). If we have a function, GCD() that returns the
greatest common denominator of its two arguments, then the sequence element a(n) would have GCD(a(n), a(n-1)) = 1 and GCD(a(n), a(n-2)) > 1.
The first few elements of integer sequence A098550 are 1, 2, 3, 4, 9, 8, 15, 14, 5, 6, 25, 12, 35, 16, 7, 10, 21, 20, 27, 22, 39, 11, 13, 33, 26, 45, 28, 51, 32, 17, 18, and 85, and a graph of its first hundred elements appears below.
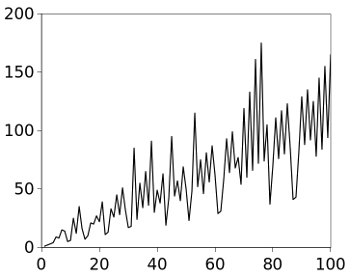
Graph of the first hundred terms of integer sequence A098550.
It looks to me more like the price chart for a volatile stock than geyser eruptions.
(Plot rendered by the author using Gnumeric.)
computers have enabled the practice of
experimental mathematics, and we can better see some properties of this sequence if we crank out more terms. For this purpose, I've written a
program in the
C language (source code,
here).
My usual
caveats, that I'm not a
professional programmer and that there are likely better ways to write such a program, apply. However, the program is short, easily understood, and it computed 20,000 elements in just a few seconds on my
desktop computer.
David Applegate, another author of the arXiv paper, has written a more elegant
C++ program.[2] The first 10,000 terms of integer sequence A098550, as calculated by my program, appear in the plot below.
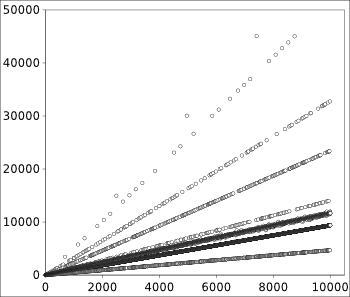
(Plot rendered by the author using Gnumeric.)
(Click for larger image)
As can be seen by inspection, the elements of the sequence seem to fall on
straight lines. When a quarter of a million points are analyzed, the
slopes of these lines are approximately 0.467, 0.957, 1.15, 1.43, 2.40, 3.38, 5.25 and 6.20. You can just barely see traces of the eighth line in the above graph. Most interestingly, if we ignore the line with slope 1.15, the ratios of the other slopes are quite nearly consecutive primes.
| | Line | Slope | Slope(n)/Slope(n-1) |
| | A | 0.467 | |
| | B | 0.957 | 2.049 |
| | D | 1.430 | 3.062 |
| | E | 2.400 | 5.139 |
| | F | 3.380 | 7.238 |
| | G | 5.250 | 11.242 |
| | H | 6.200 | 13.276 |
The arXiv paper has an
hypothesis to explain this result, and much more
analysis of integer sequence A098550.[1]
Now that you're conversant with the Yellowstone sequence, you might want to explore the properties of Recamán's sequence,
A005132, which has a similar constructor. Elements of this sequence are calculated as follows:
a(0) = 0
For n > 0:
a(n) = a(n-1) - n if positive and not already in the sequence
Otherwise a(n) = a(n-1) + n.
The first few terms of this sequence are 0, 1, 3, 6, 2, 7, 13, 20, 12, 21, 11, 22, 10, 23, 9, 24, 8, 25, 43, 62, 42, 63, 41, 18, 42, 17, 43, 16, 44, 15, 45, 14, 46, 79, 113, 78, 114, and 77.
Unlike the Yellowstone sequence, which has each natural number included just once, this sequence has duplicates. The first example of this is that terms a(20) and a(24) are both 42. A graph of the first 100,000 elements appears below.
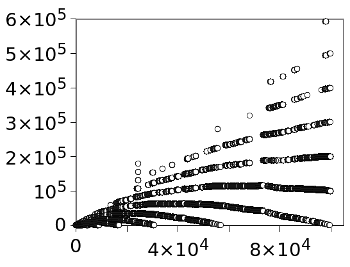
Graph of 100,000 terms of integer sequence A005132 (Recamán's sequence).
(Plot rendered by the author using Gnumeric.)
![]()
References:
- David L. Applegate, Hans Havermann, Bob Selcoe, Vladimir Shevelev, N. J. A. Sloane, and Reinhard Zumkeller, "The Yellowstone Permutation," arXiv, January 7, 2015.
- David Applegate, A C++ program to compute terms of integer sequence A098550.
- N. J. A. Sloane, The first 100000 terms of integer sequence A005132.
Permanent Link to this article
Linked Keywords: STEM fields; mathematics; number theory; parent; child; children; natural number; Unicode; integer sequence; A000027; The On-Line Encyclopedia of Integer Sequences; computer scientist; A001477; collegiality; colleague; A181975; daydream; sleep; A001745; boredom; boring; prime number; A000040; divisor; arXiv; mathematician; Neil J. A. Sloane; A098550; Cartesian coordinate system; graph; geyser; Yellowstone National Park; park; U.S. state; Wyoming; parity; even; odd; Old Faithful geyser; meter; Wikimedia Commons; greatest common denominator; chart pattern; price chart; volatility; volatile; stock; Gnumeric; computer; experimental mathematics; computer programming; C language; a098550.c; caveat; professional; programmer; desktop computer; David Applegate; C++; mathematical jargon; proof by inspection; straight line; slope; hypothesis; analysis; A005132.