Fermi-Pasta-Ulam
April 20, 2015
Of all the
scientific disciplines,
physics is the most
mathematical. It's apparent, as
Eugene Wigner wrote in 1960, that
mathematics is unreasonably effective in describing the world around us.[1] The use of mathematics in the
natural sciences can be traced back at least as far as the
third century BC, when
Greek mathematician, Eratosthenes, used trigonometry to determine the radius of the Earth to within two percent of its established value.
Physicists were quick to use the first
computers, including
mechanical calculators made by
Marchant and
Friden. During the
Manhattan Project, several
wives of the
Los Alamos scientists, including
Edward Teller's wife, Mici, acted as
human computers by doing
calculations on such machines.[2] The versatile
Richard Feynman acted as a
de facto calculator
repairman. Feynman teamed for calculator repair with
Nicholas Metropolis. Metropolis was instrumental in early physics computing, as I wrote in a
previous article (Nicholas Metropolis, June 11, 2010).
As Feynman wrote in his book,
Surely You're Joking, Mr. Feynman!, Los Alamos eventually obtained an
IBM punched-card computer.[3] This type of computer had proven its worth in calculating
planetary orbits, so it was a safe bet. The first task of the Los Alamos IBM computer was a calculation to simulate a
shaped-charge implosion. As a test of the efficacy of this new machine, the calculations were done simultaneously by both the ladies on the calculators and the IBM computer. The ladies were able to calculate at the same pace, but the IBM could function continually, without rest, so it won the
competition.[3-4]
John von Neumann, who originated the shaped-charge idea, had an early interest in computers, and he arranged to have an
unclassified Los Alamos calculation computed on the
Harvard University Mark I electromechanical calculator. The Mark I took longer to calculate, but it did the calculation with more
precision than the Los Alamos IBM computer.[2] Von Neumann was subsequently involved with
ENIAC, the first
electronic general-purpose computer, and its successor, the 6,000
vacuum tube EDVAC, one of the first
stored-program computers.

Shrinking computer hardware, ENIAC (left) and successors. The smallest circuit board is from the BRLESC-I.
(U.S. Army Photo 163-12-62, via Wikimedia Commons.)
At Los Alamos, Feynman was a pioneer in
parallel computing. By interleaving colored punch-cards containing different calculations, Feynman was able to do several computations at one time.[3] After the
war, progress in computing continued at Los Alamos, with Metropolis building the
MANIAC (mathematical analyzer, numerical integrator and computer) in 1952.[2] The MANIAC was a stored program computer.[4]
Software progress was made, also, with von Neumann, Metropolis, and
Stanislaw Ulam inventing the
Monte Carlo method.[2,5] Ulam, whose
uncle enjoyed
gambling at the
Monte Carlo casino, gave the method its name.[4]
Physicists enjoy their
play as much as their
work. Feynman would "
crack" the
safes at Los Alamos while he was there, an adventure simplified by the fact that few safe owners ever changed the default
combination.[3] In 1956, Paul Stein and Mark Wells, reportedly with assistance from
John Pasta, later head of the department of
computer science at the
University of Illinois at Urbana-Champaign, created a simplified
chess program, called "
Los Alamos Chess."[4,6] Because of the limited capability of MANIAC I, the game had a 6x6
chess board, and there were no
bishops. The game was good enough to beat at least some
humans.[4]
Pasta collaborated in a significant physics
simulation with Fermi and Ulam, now called the
Fermi-Pasta-Ulam Problem (FPU).[7-10] Physicists are always interested in the behavior of simplified model systems, as illustrated by the
particle in a box problem in
quantum mechanics. In 1953, Fermi proposed a computer simulation of the
temporal evolution of the motion of a
vibrating nonlinear string that's initially excited into a
single oscillatory mode.[7] This would be one way to simulate how
heat is conducted in
solids.
Fermi and Ulam expected that the energy of this mode would be transferred to other modes, and that this
equilibrium state would happen after a short
relaxation time. Instead, after an initial
damping of the original mode, it returned to its higher
amplitude, a feature of interacting
solitons. Of course, everyone blamed some computer error, but they found that the result was real.[7] Fermi died in 1954, but this computer simulation was published in a 1955 Los Alamos
technical report. Later, after much longer simulations, it was found that an equilibrium state is finally attained, but the way the system attains this equilibrium was not understood.[8-10]

Enrico Fermi (1901-1954).
This is my favorite photo of Fermi. He might be smiling because he's just written an incorrect expression for α, the fine-structure constant.
In cgs units, it would be e2/(ħc))
An international team of physicists and
mathematicians from the
Università degli Studi di Torino and
Istituto Nazionale di Fisica Nucleare–Sezione Torino (
Turin, Italy), the
University of East Anglia (Norwich, United Kingdom), and
Rensselaer Polytechnic Institute (Troy, New York) has now explained the eventual emergence of
equipartition of energy states in the FPU model system.[8-10] They developed a general approach to such problems, so their method can be applied to other weakly nonlinear
dispersive waves.[8]
What Fermi, Pasta, and Ulam had expected from their calculation was that their model system would reach
thermal equilibrium, a state in which the system energy would
partition itself among all possible modes. When the model ran, it appeared that the energy, stored in just a single mode as an initial condition, was being distributed. However, after subsequent
iterations it was found that the energy would periodically be dispersed, but then reconcentrated in the initial mode to about 97% of its value.[9] The development of more powerful computers allowed the simulation to proceed to much longer time scales, and it was found that thermal equilibrium did occur, but by an unknown mechanism.[10]
The model system is a linear chain of 16, 32, or 64
masses connected by a
nonlinear quadratic spring.[9] The
research team attacked the problem by methods known to work in
wave turbulence theory.[10] As it turns out, there's a mixing of modes in the system in which coincidences of modes allows a gradual transfer of energy. When precisely six modes interact, there's an
irreversible transfer of energy, but it takes many iterations to transfer enough energy to reach thermal equilibrium.[8-9]
For small-amplitude
random waves, such a mode interaction occurs on an extremely long timescale. It was found that the timescale is of the
order of
1/ε8, where
ε is a very small
system parameter.[8] The mode mixing does not have a
threshold, and the equipartition of energy will happen even for small nonlinearity.[8] Says
Yuri Lvov, an
author of the paper and a
professor of
mathematical sciences at Rensselaer Polytechnic Institute,
"My collaborators and I have shown that interactions of triads, quartets, and quintets are reversible; in other words, they do not bring the FPU system closer to thermal equilibrium. However, the interaction of waves in sixtets does lead to irreversible transfer of energy. It takes the cooperation of six different waves to produce an interaction that is irreversible and, because of that, the process is extremely weak and very slow. That is why it takes so long to approach thermal equilibrium for the FPU system."[9]
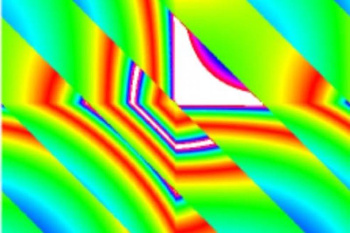
Pretty picture.
This is a visualization of the resonance manifold in the Fermi-Pasta-Ulam problem.
(RPI image by Yuri Lvov.)
![]()
References:
- Eugene P. Wigner, "The unreasonable effectiveness of mathematics in the natural sciences," Communications on Pure and Applied Mathematics, vol. 13, no. 1 (February 1960), doi:10.1002/cpa.3160130102, pp. 1-14. An online transcription is available, here, and a PDF file is available here.
- Manhattan Project History - Evolving from Calculators to Computers, The Manhattan Project Heritage Preservation Association, Inc..
- Richard Feynman, "Surely You're Joking, Mr. Feynman! (Adventures of a Curious Character)," W. W. Norton & Company, April 17, 1997, 352 pp. (via Amazon)
- Computing and the Manhattan Project, Atomic Heritage Foundation.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller, and E. Teller, "Equation of State Calculations by Fast Computing Machines," Journal of Chemical Physics, vol. 21, no. 6 (1953), pp.1087-1092. For a review of this paper, see its Wikipedia page.
John R. Pasta (1918 – June 5, 1981), Chess Programming at Wikispaces.
- Thierry Dauxois, "Fermi, Pasta, Ulam, and a mysterious lady," Physics Today, January, 2008, pp. 55-57 (PDF File).
- J.A.N. Lee, "Computer Pioneers - John R. Pasta," IEEE Computer Society.
- Miguel Onorato, Lara Vozella, Davide Proment, and Yuri V. Lvov, "Route to thermalization in the α-Fermi–Pasta–Ulam system," Proc. Natl. Acad. Sci., Published online before print, March 24, 2015, doi: 10.1073/pnas.1404397112
- Mary L. Martialay, "A Mathematical Explanation for the Fermi-Pasta-Ulam System Problem First Proposed in 1953," Rensselaer Polytechnic Institute Press Release, March 23, 2015.
- UEA mathematician solves 60-year-old problem, University of East Anglia Press Release, March 23, 2015.
Permanent Link to this article
Linked Keywords: Science; scientific; discipline; physics; mathematics; mathematical; Eugene Wigner; The Unreasonable Effectiveness of Mathematics in the Natural Sciences; mathematics is unreasonably effective; natural science; third century BC; Greek; mathematician; Eratosthenes; trigonometry; radius of the Earth; physicist; computer; mechanical calculator; Marchant calculator; Friden, Inc.; Manhattan Project; wife; Los Alamos National Laboratory; Edward Teller; human computer; calculation; Richard Feynman; maintenance, repair, and operations; repairman; Nicholas Metropolis; Surely You're Joking, Mr. Feynman!; IBM; punched-card; planetary orbit; shaped-charge; implosion; competition; John von Neumann; classified information; unclassified; Harvard University; Harvard Mark I electromechanical calculator; precision; ENIAC; electronic; vacuum tube; EDVAC; stored-program computer; computer hardware; ENIAC; BRLESC-I; Wikimedia Commons; parallel computing; World War II; MANIAC I; software; Stanislaw Ulam; Monte Carlo method; uncle; gambling; Monte Carlo casino; play; profession; work; safe-cracking; safe; combination lock; John Pasta; computer science; University of Illinois at Urbana-Champaign; chess engine; chess program; Los Alamos Chess; chessboard; chess board; bishop; human; computer simulation; Fermi-Pasta-Ulam Problem; particle in a box; quantum mechanics; time evolution; temporal evolution; vibrating; nonlinear; string; normal mode; single oscillatory mode; heat; solid; thermodynamic equilibrium; equilibrium state; relaxation time; damping; amplitude; soliton; technical report; Enrico Fermi (1901-1954); fine-structure constant; cgs units; mathematician; University of Turin; Università degli Studi di Torino; Istituto Nazionale di Fisica Nucleare–Sezione Torino; Turin, Italy; University of East Anglia (Norwich, United Kingdom); Rensselaer Polytechnic Institute (Troy, New York); equipartition theorem; equipartition of energy states; acoustic dispersion; dispersive waves; thermal equilibrium; partition function; iteration; mass; linearity; nonlinear; quadratic function; spring; research; wave turbulence; irreversible process; thermodynamics; irreversible; randomness; random; orders of approximation; order; system; parameter; threshold; Yuri Lvov; author; professor; mathematical sciences; scientific visualization; resonance; manifold.