Topological Insulators and Stanene
February 24, 2013
The name of
physicist,
Enrico Fermi, is attached to many things, one of these being the
Fermi level. The Fermi level, often symbolized as
μ, is the
energy level that would be occupied by
electrons half the time at
thermodynamic equilibrium. The
probability f(ε) of an electron being at any particular energy level,
ε, at temperature,
T, is given by the
Fermi-Dirac distribution,
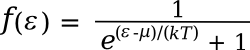
where
k is the
Boltzmann constant. It's easy to see from this
equation that a probability of one-half is obtained when the energy is the Fermi level energy; that is, when
ε-μ = 0).
There's no requirement that a
solid must have electrons at the Fermi level. It just describes how electrons at that level would behave. In the
band theory of solids, the location of the Fermi level with respect to the
energy bands of a material determines the material's
electrical conductivity.
Insulators have a large
band gap between the energy of their
valence electrons, residing in a
valence band, and
conduction electrons, residing in a
conduction band. The Fermi level sits within this gap, and there are few electrons with sufficient energy to jump the gap. In a
metal, the Fermi level is within the conduction band, so there are electrons available for conduction. In
semiconductors, the Fermi level is outside the conduction band, but it's close enough for electrons to be excited into the conduction band to allow some conduction.
This tutorial is prologue to a description of an interesting type of insulator, the
topological insulator.[1-3] As the figure shows, these have a Fermi level between the valence band and the conduction band, as in other insulators. However, their
surface electrons have a different trajectory in energy-
momentum space, so these materials are bulk insulators and surface conductors at the same time.
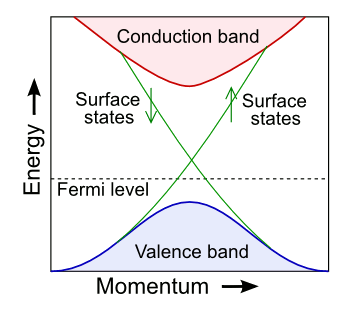
Simplified band structure of a topological insulator.
(Modified image by "A13ean," via Wikimedia Commons.)
This is not that surprising, since
atoms at a surface will have "
dangling bonds,"
electron orbitals which would
bond to adjacent atoms if any were present. These unemployed electrons (at least the
anthropomorphic kind) are looking for a new job, and for the topological insulators this new job is conducting current along their surfaces. This strange property is a result of two
quantum mechanical principles; namely,
time-reversal symmetry and a
spin–orbit coupling which exists in
heavy elements such as
mercury and
bismuth.
In fact, the first demonstration of a topological insulator was in a compound of mercury. This was a thin layer of
mercury telluride (HgTe) sandwiched between between layers of
mercury cadmium telluride (Hg
xCd
1–xTe). It was shown that the conductivity of the sandwich was independent of the width, confirming that the conductance was at the
edges, only. Shortly thereafter,
three-dimensional topological insulation was found in
bismuth selenide (Bi
2Se
3) and
bismuth telluride (Bi
2Te
3).
There's a lot of
physics in topological insulators. The
spins of the conducting electrons are aligned with the direction of
current flow, so they're not easily scattered by
defects or
impurities. The interaction of an electron's spin and
orbital angular momentum in heavy elements, such as Bi, is so strong that there's an inversion of the energy gap in topological insulators, with high energy states appearing below the gap. This results in metallic conduction at the surface.[3]
The same
research team that predicted that these mercury and bismuth compounds would be topological insulators have recently made another prediction. Although
tin (
atomic number 50) is a lighter element than mercury (atomic number 80) or bismuth (atomic number 83), it's theorized that a single layer of tin (
stanene), if produced, would be a topological insulator. It's further predicted that modification of the tin layer with
fluorine will give the additional property that the surface electrons will mimic
superconductivity at
room temperature and higher
temperatures.[4-8]
The team of
theoretical physicists involved in this work is led by members of the
SLAC National Accelerator Laboratory and
Stanford University.[5] Other team members are from
Tsinghua University (Beijing) and the
Max Planck Institute for Chemical Physics of Solids (Dresden, Germany). Their first-principles calculations show that two-dimensional tin films are
quantum spin Hall insulators with a bandgap for the bulk material of 0.3
eV.[4]
The properties of these films can be tuned by attachment of other chemical species to the tin atoms.[4] Calculations show that a layer of tin a single atom in thickness would be a topological insulator at and above room temperature, and attaching fluorine atoms to the tin atoms would extend its operating range to at least 100°
C (see figure).[5] Attachment of
hydrogen removes the topological property to produce an insulator, but topological insulators could be made by attachment of
I,
Br,
Cl,
F or
OH.[4]
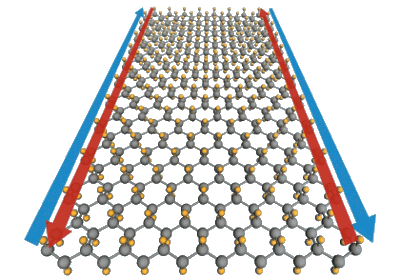
In this illustration, tin atoms (gray) are decorated with fluorine anions (yellow).
Fluorine is predicted to make this a superconducting topological insulator.
(Yong Xu/Tsinghua University; Greg Stewart/SLAC.)
Says team leader,
Shoucheng Zhang, a
professor of physics at Stanford and the
Stanford Institute for Materials and Energy Sciences, a joint institute with SLAC,
"Stanene could increase the speed and lower the power needs of future generations of computer chips, if our prediction is confirmed by experiments that are underway in several laboratories around the world... Eventually, we can imagine stanene being used for many more circuit structures, including replacing silicon in the hearts of transistors... Someday we might even call this area Tin Valley rather than Silicon Valley."[5]
References:
- Charles Kane and Joel Moore, "Topological insulators," Physics World, February, 2011, pp. 32-36 (PDF file).
- Michel Fruchart and David Carpentier, "An Introduction to Topological Insulators," arXiv Preprint Server, November 3, 2013. Available, also, as Michel Fruchart and David Carpentier, "An Introduction to Topological Insulators," Comptes Rendus Physique, vol. 14, nos. 9-10 (November–December, 2013), pp. 779-815.
- Ali Yazdani, "Topological Insulators - Overview," Princeton University Web Site.
- Yong Xu, Binghai Yan, Hai-Jun Zhang, Jing Wang, Gang Xu, Peizhe Tang, Wenhui Duan and Shou-Cheng Zhang, "Large-Gap Quantum Spin Hall Insulators in Tin Films," Physical Review Letters, vol. 111, no. 13 (September 27, 2013), Document No. 136804 [5 pages] . Available, also, from arXiv.
- Will 2-D Tin be the Next Super Material?, SLAC Press Release, November 21, 2013.
- Will 2D tin be the next super material for chip interconnects?, Kurzweil Accelerating Intelligence, November 25, 2013.
- Charles Q. Choi, "Could Atomically Thin Tin Transform Electronics?," Scientific American, December 4, 2013.
- Rik Myslewski, "OHM MY GOD! Move over graphene, here comes '100% PERFECT' stanene," The Register (UK), December 4, 2013.
Permanent Link to this article
Linked Keywords: Physicist; Enrico Fermi; Fermi level; energy level; electron; thermodynamic equilibrium; probability; Fermi-Dirac distribution; Boltzmann constant; equation; solid; electronic band structure; band theory of solids; energy band; electrical conductivity; insulator; band gap; valence electron; valence band; conduction electron; conduction band; metal; semiconductor; topological insulator; surface; momentum; A13ean; Wikimedia Commons; atom; dangling bond; molecular orbital; electron orbital; chemical bond; anthropomorphism; anthropomorphic; quantum mechanics; quantum mechanical; T-symmetry; time-reversal symmetry; spin–orbit coupling; heavy element; mercury; bismuth; mercury telluride; mercury cadmium telluride; edge; three-dimensional; bismuth selenide; bismuth telluride; physics; spin; electric current; crystallographic defect; impurity; orbital angular momentum; research; tin; atomic number; stanene; fluorine; superconductivity; room temperature; temperature; theoretical physics; theoretical physicist; SLAC National Accelerator Laboratory; Stanford University; Tsinghua University (Beijing); Max Planck Institute for Chemical Physics of Solids (Dresden, Germany); Quantum spin Hall effect; electronvolt; eV; Celsius; C; hydrogen; iodine; I; bromine; Br; chlorine; Cl; fluorine; F; hydroxide; OH; Yong Xu; Greg Stewart; Shoucheng Zhang; professor; Stanford Institute for Materials and Energy Sciences; integrated circuit; computer chip; experiment; silicon; transistor; Silicon Valley.