The Traveling Salesman Problem
March 1, 2013
Pen plotters were a common feature in
laboratories several decades ago.
Servomotors would move
wire and
pulley assemblies to drag a
pen across a piece of
paper pre-printed with a
graph ruling. The early pens were recharged with
liquid ink, which often seemed to be more worrisome than the
hazardous chemicals we handled daily. We were happy when these were replaced in newer units by
felt-tipped pens.

When
computers made their way into laboratories, the pen plotters were still there, but they were
interfaced digitally. Somewhere around 1990,
graphics printers were low enough in cost that pen plotters were finally abandoned, and graphs were printed from sophisticated
computer programs, graph ruling, legends, and all.
The image on the left might look like an errant pen plotter trace in which the voltage connections were loosened by too many tugs from the electrode wires of a laboratory mouse. You may notice, however, the resemblance to my head shot at the top of this page.
This image is formed from a single line, so it could have been made by a pen plotter. The line is close to the shortest route through the 8,386 points in a monochrome stippling of the color photo. Finding the shortest such route is called the
traveling salesman problem (TSP). Instructions for making images like this can be found on the interestingly named
Evil Mad Scientist web site.[1-2]
The traveling salesman problem is based on the simple idea that a
salesman would rather be selling than traveling, so he tries to keep the distance between his stops as short as possible by visiting his customers in a logical fashion. The TSP was introduced in 1930, long before digital computers. At that time, the
mathematician,
Karl Menger, made the following observation:
"The rule that one first should go from the starting point to the closest point, then to the point closest to this, etc., in general does not yield the shortest route."[3]
The traveling salesman problem is the most studied
optimization problem because it can be generalized to things other than selling, such as routing
conductors on an
integrated circuit. The concept of distance can be generalized to cost, as in determining the lowest cost route for a
pipeline,
highway, or
optical cable for a given
terrain.
Ubiquitous computing makes such analysis practical.
The computer program that did the routing for my image is written in the
Python programming language. It solved a route very close to the TSP solution in about a minute on my very ancient, but still serviceable, 3.2 GHz
AMD Sempron™ Linux system. This doesn't sound like too long of a time for so many thousands of points; but many problems have many more points, and a
real TSP, which implies
the shortest route, is not easy; in fact, it's officially
hard, since it's a member of a class of problems known as "
NP-hard," a result found by
computer scientist,
Richard Karp, in 1972,[4]
The solution for a 49-city TSP was done by computer in the 1950s, followed by a 2,392-city map in the 1980s, 13,509 cities in 1998 (see figure), and an integrated circuit routing problem of 85,900-nodes at
Bell Labs in 2006.[4] Despite these successes, it appears that the worst-case run time for a TSP-solving
algorithm is
exponential in the number of points. This is not a happy result, since people are hoping to find something like a
linear time algorithm.
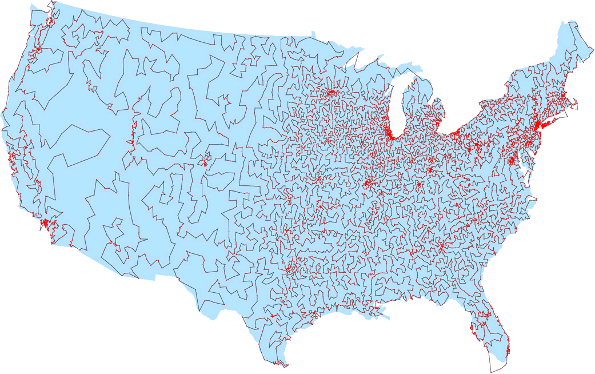
The shortest traveling salesman route calculated for the 13,509 cities in the contiguous United States with a population of at least 500 in 1998. (Simons Foundation image Courtesy of David Applegate, Robert Bixby, Vasek Chvatal and William Cook)
Perfection is nice, but when it's not readily obtainable,
approximations are often worthwhile. In 1976,
Nicos Christofides of the
Imperial College London, found an algorithm which guarantees a route with a worst-case routing that's only 50% longer than a perfect TSP. His approach was to find the shortest
spanning tree, the connections linking cities without generating closed loops. The spanning tree generates a
maze which gives a TSP solution that's at worst twice the best route when traveled, but only 50% longer when optimized.[4]
Surprisingly, this was the best algorithm for the next few decades until a team from
Stanford University and
McGill University was able to shave the merest fraction from that percentage in 2011.[4] This result, made possible by the introduction of
randomness into the calculations, had just a small practical consequence, but it encouraged further
research into finding better TSP approximations. The approximations now generate a worst-case route that's just 40% larger than a perfect TSP routing.[4]
Sanjeev Arora, a computer scientist at
Princeton University, is quoted in a
Simons Foundation press release as saying,
"Mathematical discovery is like feeling your way in a dark room: putting your hand here and finding a chair, putting your hand there and finding a table... At some point, your hand hits the light switch, and suddenly everything makes sense. For the traveling salesman problem, even after so many papers that have pushed the envelope in so many directions, I don't think that we have hit that switch yet."[4]
Of course, the idea of a salesman traveling between as few as five cities in a day is rather extreme, but foraging
bumblebees will visit many
flowers in a single day. Although handheld computing devices have become smaller, bumblebees still don't have computers. However, research does indicate that they have an
instinctive TSP algorithm that assists their foraging. The bumblebees, not unlike salesmen, also include the value of their targets as well as their distance. This research, by scientists at
Queen Mary, University of London's School of Biological and Chemical Sciences, is published in the
British Ecological Society's journal,
Functional Ecology.[5-6]
To eliminate
extraneous variables, the research team used artificial, rather than real, flowers, charged with specific
nectar rewards. Other research has found that bees will follow repeatable sequences, called
trap-lines, when
foraging, since flowers need time to refill with nectar. Individual bees were tagged so they could be tracked, and they were given access to five artificial flowers arranged in a
regular pentagon.[5-6] Said study coauthor,
Mathieu Lihoreau,
"When the flowers all contain the same amount of nectar bees learned to fly the shortest route to visit them all... However, by making one flower much more rewarding than the rest we forced the bees to decide between following the shortest route or visiting the most rewarding flower first."[6]
It was found that if the increased distance for the greater reward was not that great, the bees would visit the high value target first. There was a point at which the distance became too large to compensate for the extra travel. If the increase in distance for the overall route was less than 18%, the bees would always go to the high value flower first. When this climbed to 42%, the shortest route was taken.[5]

Ventral view of a Bombus terrestris (bumblebee), posing as if in a made-for-TV science fiction movie.
Killer Bees was a 1974 made for TV film, the plot of which involved a woman with psychic control of a swarm of Africanized bees ("killer bees").
Photo by Bernd Lang, via Wikimedia Commons.)
![]()
References:
- Producing a stippled image with Gimp, Evil Mad Science Wiki.
- Generating TSP art from a stippled image, Evil Mad Science Wiki.
- Paul Muljadi, Ed., Introduction to Graphs, Example Applications of Graph Theory, "Travelling Salesman Problem," pp. 94 ff.
- Erica Klarreich, "Computer Scientists Take Road Less Traveled," Simons Foundation Press Release, January 29, 2013.
- Mathieu Lihoreau, Lars Chittka and Nigel E. Raine, "Trade-off between travel distance and prioritization of high-reward sites in traplining bumblebees," Functional Ecology, vol. 25, no. 6 (December 2011), pp. 1284-1292 .
- How bumblebees tackle the traveling salesman problem, Queen Mary, University of London, Press Release, June 28, 2011.
Permanent Link to this article
Linked Keywords: Pen plotter; laboratory; servomotor; wire rope; wire; pulley; pen; paper; graph paper; graph ruling; liquid ink; hazardous chemical; felt-tipped pen; computer; IEEE-488; interfaced digitally; graphics printer; computer program; voltage; electrode wire; laboratory mouse; head shot; monochrome; stippling; traveling salesman problem; travelling salesman problem; Evil Mad Scientist; salesman; mathematician; Karl Menger; optimization problem; electrical conductor; integrated circuit; pipeline transport; pipeline; highway; optical fiber cable; optical cable; terrain; ubiquitous computing; Python programming language; Advanced Micro Devices; AMD; Sempron™; Linux; NP-hard; computer scientist; Richard Karp; Bell Labs; algorithm; exponential time; time complexity; linear time; contiguous United States; population; Simons Foundation; David Applegate, Robert Bixby, Vasek Chvatal and William Cook; approximation; Nicos Christofides; Imperial College London; spanning tree; maze; Stanford University; McGill University; randomness; research; Sanjeev Arora; Princeton University; James Harris Simons; bumblebee; flower; instinct; instinctive; Queen Mary, University of London; School of Biological and Chemical Sciences; British Ecological Society; scientific journal; Functional Ecology; extraneous variable; nectar; trap-line; foraging; regular pentagon; Mathieu Lihoreau; television film; made-for-TV; Killer Bees; Africanized bees; Bombus terrestris; Wikimedia Commons; Evil Mad Science Wiki.