Proton Size Problem
March 20, 2013
The
subatomic particle of the moment is the
Higgs Boson, which apparently has been discovered in
experiments at the
Large Hadron Collider. More
data needs to be forthcoming to confirm the
spin of the particle detected (The Higgs would have a spin of zero), but it appears to be the particle predicted by the
Standard Model. Having
theory precede experiment is a good position. As
Arthur Eddington once
cautioned," It is also a good rule not to put overmuch confidence in the observational results that are put forward until they are confirmed by theory."
Far less exotic than the Higgs boson is the
proton, discovered nearly a
century ago by
Ernest Rutherford. Over the course of that century, the proton was demoted from an
elementary particle to a
composite particle composed of three
quarks (two
up quarks and one
down quark). Whereas an
electron is quite nearly a
point particle, the composite nature of the proton gives it a size.
As Rutherford's scattering experiments demonstrated, protons acts as if they were charged
spheres. The edge of the sphere is not sharply defined, so the
charge radius is taken as a
root-mean-squared value. There have been many measurements of this charge radius, and the accepted value is 0.8768
femtometers (fm).[1]
Until July, 2010, all such measurements were done using the interaction between protons and electrons, either by electron-proton scattering, or by
spectroscopy of
hydrogen atoms. electron-proton scattering was the first such measurement, and it was important enough that
Robert Hofstadter shared the 1961
Nobel Prize in Physics.
The other method involves spectroscopy of the energy levels of neutral hydrogen. The neutral hydrogen atom consists of a
nucleus of only one proton associated with a single electron, so it's a very simple system. These two independent measurements allowed a good estimate of the proton charge radius. While not as accurately determined as the value for other physical constants, it was known to within a percent.
All this certainty vanished in July, 2010, when a different sort of measurement showed a significantly smaller proton charge radius.
As I wrote in a
previous article (Fat Protons, July 12, 2010), measurements on an analog of the hydrogen atom in which a
muon replaces the electron gave a proton charge radius of only 0.84184 fm.[2-5] This was five
standard deviations from the established value. A repeat of this measurement has just yielded 0.84087 fm with a precision that places the established value seven standard deviations too high.[6-8]
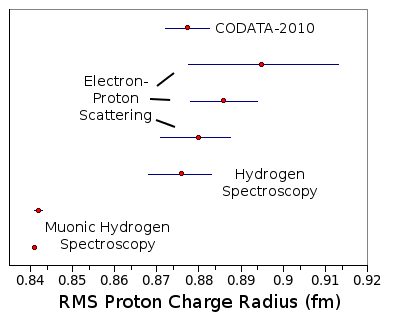
Proton radius values, as determined by different methods.
Note the small standard deviation bars for the muonic hydrogen data.
(Plotted with Gnumeric, using data from ref. .)
The measurements are done using pulsed laser
spectroscopy of the
Lamb shift of muon energy levels in muonic hydrogen. It's possible to calculate the proton radius using the measured Lamb shift.[9] The Lamb shift, named after
Nobel Physics Laureate,
Willis Lamb, is the small difference in energy between the
2S
1/2 and
2P
1/2 electron energy levels.
Muonic hydrogen, as shown in the figure, is an analog of hydrogen that has a proton orbited by a negative
muon.
In principle, muonic hydrogen provides a better system than hydrogen for measurement of the proton charge radius. This is because the muon, which has about 200 times the
mass of an electron, travels (in the
Bohr model sense) nearer to the proton than an electron.
Aldo Antognini, lead author of the
Science paper describing these results, says that the precision of the muonic hydrogen measurement is an
order of magnitude better than previous measurements.[8] The relative accuracy is 5x10
-4.[8]
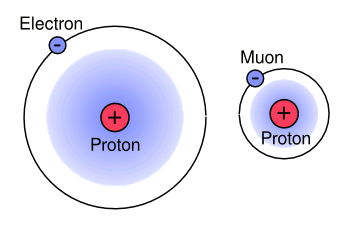
The Bohr models of hydrogen and muonic hydrogen drawn to scale.
(Illustration by the author using Inkscape.)
The essential experimental problem, and the reason why such experiments have been done just recently, is that muons exist for just two
milliseconds. In such a short time span, you need to create muonic hydrogen and measure the Lamb shift. The international research team, whose membership included
scientists from thirteen institutions, was able to generate a few hundred muons each second, a small fraction of which replaced electrons in hydrogen gas.
What should we make of this result? It appears that the experiments were done with due care, but there's a lot of
mathematics between the Lamb shift measurement and the estimate of the proton charge radius.[8] The
Rydberg constant, which is used in the
equations, might be wrong.[5] Also, there might be something about the structure of the proton that gives one value for muons, and another for electrons. It's certainly too early to be thinking that there's some fundamental error in
quantum electrodynamics.
Waxing
philosophical, we still don't understand why a proton should have a particular charge radius. Also, as a spinning ball of charge, the proton has a
magnetic moment. The reason for its value is still unknown, but the muonic hydrogen experiments give a magnetic radius of 0.87 fm.[6] What's especially interesting is that this smaller proton charge radius increases the
charge density of protons by about thirteen percent.
References:
- NIST, "CODATA Value: proton rms charge radius," (June, 2011).
- Randolf Pohl, et al., "The size of the proton," Nature, vol. 466, no. 7303 (July 8, 2010), pp. 213-216.
- Thomas H. Maugh II, "Physics: Proton radius smaller than believed, European scientists say," Los Angeles Times Online, July 7, 2010.
- Lisa Grossman, "'Horrendously Intense' Laser Shrinks the Proton," Wired, July 7, 2010.
- Kate Ravilious, "Proton Smaller Than Thought-May Rewrite Laws of Physics," National Geographic Online, July 7, 2010.
- Aldo Antognini, et al. "Proton Structure from the Measurement of 2S-2P Transition Frequencies of Muonic Hydrogen," Science, vol. 339 no. 6118 (January 25, 2013), pp. 417-420.
- Helen S. Margolis, "How Big Is the Proton?" Science, vol. 339 no. 6118 (January 25, 2013), pp. 405-406.
- Science Podcast transcript, Science, vol. 339 no. 6118 (January 25, 2013), p. 468. Host Sarah Crespi Interviews Aldo Antognini.
- Aldo Antognini, Franz Kottmann, Francois Biraben, Paul Indelicato, Francois Nez, Randolf Pohl, "Theory of the 2S-2P Lamb shift and 2S hyperfine splitting in muonic hydrogen." Arxiv Preprint Server, Novemner 20, 2012.
Permanent Link to this article
Linked Keywords: Subatomic particle; Higgs Boson; experiment; Large Hadron Collider; data; spin; Standard Model; theory; Arthur Eddington; proton; century; Ernest Rutherford; elementary particle; composite particle; quark; electron; point particle; sphere; charge radius; root-mean-square; femtometer; spectroscopy; hydrogen atom; Robert Hofstadter; Nobel Prize in Physics; nucleus; muon; standard deviation; Gnumeric; spectroscopy; Lamb shift; Nobel Physics Laureate; Willis Lamb; muonic hydrogen; muon; mass; Bohr model; Aldo Antognini; Science; order of magnitude; Inkscape; millisecond; scientist; mathematics; Rydberg constant; equation; quantum electrodynamics; philosophy; philosophical; magnetic moment; charge density; NIST; CODATA.