Early Math Education
March 18, 2013
My first remembrance of
mathematics is from
first grade. I had spent
kindergarten in one
school, and I had transferred into another for first grade. The
teacher was concerned that I didn't write the
digit,
two, properly, since I wrote it as it now appears in nearly every
typeface, as
2.
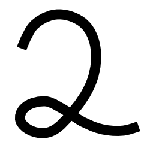
Proper
penmanship at the time required that it be written with a loop, as shown in the figure; so, while the other students were doing a real math lesson, I was required to draw twos-with-loops at the blackboard. To see how rare an object this is today, do a Google image search for "handwritten digits."
I can't remember what the other students were learning at the time, but I take consolation in the fact that those were the days before the "New Math." There was not much depth in math training in
grammar school at that time, and I probably didn't miss much. My mathematics training only started when I experienced New Math in
seventh grade.
I was in seventh grade in 1959-1060, which was just two years after the launch of
Sputnik 1 on October 4, 1957. Sputnik was the supposed stimulus for actually trying to teach children some useful
science and mathematics so they might mature into the
scientists and
mathematicians that the
US said it needed. The unfortunate thing was that many of these technically trained people couldn't find work when conditions changed in the next decade.
My New Math course taught me two topics which would prove useful in my early encounters with
computers. These were
number bases and
Boolean algebra. For some reason, the only number base we encountered above
base-10 was
base-12; and, in that case,
ten was encoded as
t and
eleven was encoded as
e, quite unlike the conventional case of using
a and
b.
An old joke among computer scientists, but a good ice breaker for instructors teaching introductory computer courses)
The best way to teach mathematics to children is still being debated. The primary reason for this is that mathematics is an immense jumble of topics passed off in one name. The same is true for
physics and other sciences. Deciding what order of topics is the best to present to young minds is the first problem, and deciding how much to teach is the second.
The concepts of
ordinal and
cardinal numbers are a good starting place, and that's why
Sesame Street has its
Count von Count character. A
vampire mathematician makes sense, since mathematicians are dedicated people who linger at their desks and don't venture outside during
daylight hours.
A recent study by
psychologists at the
University of Missouri (
Columbia, Missouri) and
Carnegie Mellon University (
Pittsburgh, Pennsylvania) has demonstrated that children who fail to acquire a basic knowledge of the number system in first grade fall behind their peers in mathematics knowledge in seventh grade. This
National Institutes of Health funded study tested the essential mathematics skills people need in
adult life.[1-2] The motivation for the study is that 20% of adults in the United States are functionally innumerate and they don't have the mathematical competency needed for many jobs.[1]
The study examined students at twelve
elementary schools in the Columbia, Missouri, school system. The first graders were tested on their knowledge of the following number system principles:
• Numbers represent different magnitudes (e.g., 3 > 2).
• Number relationships stay the same, even though numbers may vary (e.g., 11-10 = 1 and 2-1 = 1).
• The digit symbols represent quantity of items (e.g., 3 => three cookies).
• Numbers can be broken into parts in several ways (5 = 2 + 3 and 5 = 1 + 4).
The seventh grade testing was performed with 180 students who took timed tests on basic math skills that adults should have; namely, multiple-digit
addition,
subtraction,
multiplication, and
division problems; comparisons and computations with
fractions; and
word problems. There were also veiled
algebra problems, such as the number of
coins needed to make change in a purchase. Fraction problems involved things such as doubling of
cooking recipes, or finding the
center of a wall.[2]
Low numeracy scores in first grade were a predictor of low scores on the seventh grade test. Other assessments showed that the difference in numeracy between high and low performers was not related to
intelligence,
language skills or the method students used to make their computations.[2]
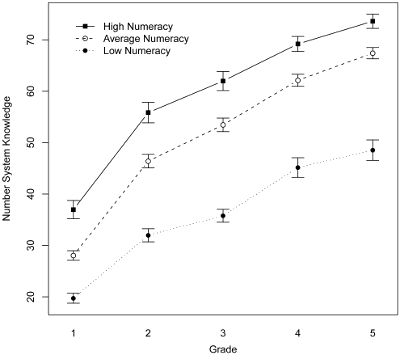
Growth in Number Systems Knowledge.
Shown are the first quartile, an average of the middle two quartiles, and the last quartile.
(Figure 2 of ref. 1, licensed under the Creative Commons Attribution License)
The study authors conclude that an early grasp of numeracy concepts was important to success in mathematics in later years, and that early efforts to help children acquire such skill could have significant long-term benefits.[1-2] Said
Kathy Mann Koepke, the director of the National Institutes of Health division that supported this research,
"An early grasp of quantities and numbers appears to be the foundation on which we build more complex understandings of numbers and calculations... These findings are especially valuable for bringing attention to the idea that numeracy early in life has profound effects not only for the individual, but also for the society that individual works and lives in."[2]
References:
- D.C. Geary, M.K. Hoard, L. Nugent, and D.H. Bailey, "Adolescents' Functional Numeracy Is Predicted by Their School Entry Number System Knowledge," PLoS ONE, vol. 8, no. 1 (January 30, 2013), doi:10.1371/journal.pone.0054651.
- First grade math skills set foundation for later math ability, National Institute of Child Health and Human Development Press Release, February 27, 2013.
Permanent Link to this article
Linked Keywords: Mathematics; first grade; kindergarten; Grammar school; teacher; numerical digit; number two; typeface; penmanship; student; blackboard; Google image search; New Math; seventh grade; Sputnik 1; science; scientist; mathematician; United States; US; computer; radix; number base; Boolean algebra; decimal; base-10; duodecimal; base-12; number ten; number eleven; mathematical joke; computer scientist; physics; ordinal number; cardinal number; Sesame Street; Count von Count; vampire; daylight hours; psychologist; University of Missouri; Columbia, Missouri; Carnegie Mellon University; Pittsburgh, Pennsylvania; National Institutes of Health; adult; elementary school; addition; subtraction; multiplication; division; fraction; word problem; algebra; coin; cooking recipe; center; Wechsler Adult Intelligence Scale; intelligence; language; quartile; Creative Commons Attribution License; Kathy Mann Koepke; PLoS ONE.