| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
The Circle Ratio
April 12, 2013
What more cruel a
fate can there be for a
child than to be born on
Christmas Day? They're never certain that the number of
gifts they receive on that one day measures up to what they would have received as a sum of gifts from another
birth date plus Christmas. Actually, one out of 1461 children might prefer a Christmas birthday to their own. They were born on
leap year day (February 29).
Strictly speaking, leap year day
babies will have a birthday (as distinct from a birth anniversary) just once every four years. We can do some
mathematical trickery to rescue their lost birthdays by doing a
mapping. We just refer to their birthday as the day after February 28; or, the day before March 1.
A recent paper on
arXiv by
mathematician,
David Richeson, of
Dickinson College (
Carlisle, PA) examines the interesting early
history of the
ratio of the
circumference C of a
circle to its
diameter D.[1] Today, we know quite a lot about this ratio,
pi (π), but in the early history of
geometry, this ratio had the amorphous character of a leap year birthday, existing in one sense, but not in another.
Richeson presents evidence that
Archimedes (287-212 BC) should be credited with the observation that the ratio of the circumference of a circle to its diameter is a
constant that's the same for all circles, large and small. This idea seems
intuitive to the modern,
mathematical mind, but early geometers had a problem because they couldn't pin a number on it. In the twenty centuries between Archimedes to
Descartes, mathematicians believed that it was impossible to find the ratio of a
curved line to a
straight line. So, how could there be a ratio describing all things circular, when the ratio is impossible to know?
Euclid (left), in a portrait by 17th century painter, Antonio Cifrondi; and, Archimedes (right). (Source images, left and right, via Via Wikimedia Commons)
The ancient
scholars were concerned about claiming the existence of something so fundamentally mysterious; that is, you claim to have a ratio, but you can't describe what that ratio is. In modern terms, this problem could be framed in the context of the
synthetic a priori.
Aristotle (384-322 BC), whose authority in all things
scientific was essentially unquestioned until a few centuries ago, stated explicitly that you can't discuss this ratio. His reasoning followed from the presumed impossibility of comparing the lengths of curves and straight lines.
Euclid (~300 BC), demonstrated in his
Elements that
(A/r2), where
A is the
area of a circle of
radius r, is a constant, but he didn't write about
(C/D) being constant. Although Archimedes proved that a circle's area is
(1/2)(C)(r), he didn't write explicitly about
C/D being a constant. This conclusion, however, is implicit in his estimate of the
C/D ratio, as discussed below.
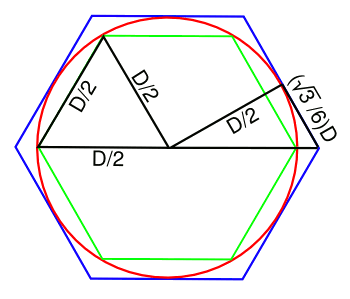
Archimedes' polygon method for estimating the ratio of the circumference to the diameter of a circle.
For inscribed and circumscribed hexagons, we get 3 ≤ π ≤ 3.464. Archimedes used 96-sided polygons to get
(223/71) ≤ π ≤ (22/7).
(Illustration by the author using Inkscape.)
The figure, above, demonstrates Archimedes' now familiar
polygon method for estimating the ratio of the circumference to the diameter of a circle. He reasoned that a polygon inscribed in a circle would always have a smaller
perimeter than circle's circumference; and, a circumscribed polygon would have a larger perimeter. Calculating for a polygon with 96 sides allowed the following estimate:
(223/71) ≤ π ≤ (22/7)
This places the value of pi between 3.14085 and 3.14286. If we average these, we get 3.141855, which is within a hundredth of a percent of the value of pi.
Richeson writes that an important part of Archimedes' method is that it involves straight lines, only. We now treat curves like
strings that can be straightened into lines, and
teachers often demonstrate the approximate value of pi by wrapping a string around a disk, and then unwrapping it against a
ruler. Ancient geometers, perhaps thinking more
mechanically than
analytically, thought that curves and lines were fundamentally different. Archimedes' method was successful, since it wasn't based on any processing of curves.
Not really defining pi, but talking around it, Archimedes showed that the circle and sphere constants were related; viz.,
π = (C/D) = (A/r2) = (6V/D3) = (1/4)(S/r2)
in which
A is the area of a circle,
V is the volume of a sphere, and
S is the surface area of a sphere.
Archimedes had so much pride in the result of his investigation, "
On the Sphere and Cylinder" (~225 BC), that he asked that it be placed on his
grave marker. He proved that when a sphere is circumscribed by a
cylinder, the
volume and surface area of the sphere are each two-thirds those of the cylinder. Two centuries later, the
Roman orator,
Cicero, discovered the
tomb, hidden by an overgrowth of
vegetation.
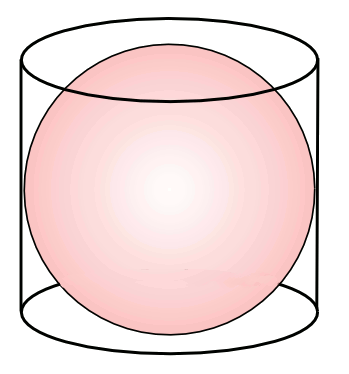
A sphere inscribed in a cylinder, the supposed inscription at Archimedes' Tomb.
Archimedes showed that the volume and surface area of the inscribed sphere are each two-thirds those of the cylinder.
This was quite a feat in the days before calculus.
(Illustration by the author using Inkscape.)
Reference:
- David Richeson, "Circular reasoning: who first proved that C/d is a constant?" arXiv Preprint Server, March 14, 2013.
Permanent Link to this article
Linked Keywords: Fate; child; Christmas; gift; birthday; birth date; leap year day; infant; baby; mathematics; mathematical; mapping; arXiv; mathematician; David Richeson; Dickinson College; Carlisle, Pennsylvania; history; ratio; circumference; circle; diameter; pi; geometry; Archimedes; constant; intuition; intuitive; Descartes; curve; curved line; straight line; Euclid; portrait; 17th century; painter; Antonio Cifrondi; Wikimedia Commons; scholar; synthetic a priori; Aristotle; science; scientific; Euclid; Elements; area; radius; polygon; hexagon; Inkscape; perimeter; string; teacher; ruler; mechanics; mechanical; mathematical analysis; analytical; On the Sphere and Cylinder; headstone; grave marker; cylinder; volume; Roman Empire; Roman; orator; Cicero; tomb; vegetation; calculus.