| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Euler Bricks
April 26, 2013
You can likely gauge the
mathematical precocity of a child by the age at which he or she exhibits knowledge of one of the many things associated with
Leonhard Euler. Euler accomplished much in his life, and he was not just an eminent
mathematician, but a
physicist who made contributions to
mechanics and
astronomy. A principal scientific contribution was his development of the
Huygens wave theory of light as a counterpoint to the
corpuscular theory in
Newton's Opticks.
A Russian two-ruble coin celebrating the 300th anniversary of Euler's birth.
The equation is Euler's identification of the Basel problem as an infinite series formula of pi.
(Via Wikimedia Commons))
Finding interesting mathematics problems was relatively easy in Euler's day, since there was so much mathematics undiscovered. You can imagine Euler taking a stroll to the market, perhaps to buy more ink, since he had just penned another lengthy treatise. He drops a coin on the roadway, and he contemplates a road
brick as he stoops to pick it up. At that point he imagines what's now called an
Euler brick.[1-3]
An Euler brick is a
rectangular cuboid whose
edges and face
diagonals all have
integer length. The edges and diagonal of any face of an Euler brick will be a
Pythagorean triple, and there are many integer
sets that comprise a Pythagorean triple.[4] The number of sets of edge lengths accessible to an Euler brick are far less, since they must satisfy the following
equations simultaneously.
a2 + b2 = d2
a2 + c2 = e2
b2 + c2 = f2
in which
a,
b and
c are the lengths of the sides, and
d,
e and
f are the diagonals, as shown in the figure. These must all be integers.
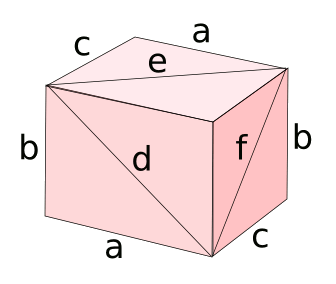
Diagram of an Euler brick.
(Created by the author using Inkscape)
Not surprisingly,
The On-Line Encyclopedia of Integer Sequences™ has three sequences associated with Euler bricks. These are the lengths of the
shortest edge, the
intermediate edge, and the
longest edge. We can imagine a more perfect Euler brick for which the space diagonal (any one of the four equivalent diagonals criss-crossing the interior space) is also an integer, but no example of such a perfect cuboid has been found.
Computer searches up to a smallest edge of 10
10 have been unsuccessful.
There are ten Euler bricks in the range (1 ≤ a ≤ b ≤ c ≤ 1000). These are listed in the table below.
| a | b | c | | a | b | c |
| 44 | 117 | 240 | | 160 | 231 | 792 |
| 85 | 132 | 720 | | 176 | 468 | 960 |
| 88 | 234 | 480 | | 240 | 252 | 275 |
| 132 | 351 | 720 | | 480 | 504 | 550 |
| 140 | 480 | 693 | | 720 | 756 | 825 |
Since I needed some
coding practice, I wrote a
program to find the dimensions of Euler bricks. You can find the
source code, albeit in my far too casual coding style,
here. The program works well for small numbers, and it wouldn't be too hard to modify it for big numbers through use of an
arbitrary-precision arithmetic library, such as the
GNU Multiple Precision Arithmetic Library.
In the introduction, I wrote about mathematics being "discovered." There's a question as to whether mathematics is invented or discovered. As I explained in a
previous article (Mathematical Objects, May 9, 2008), I'm a member of the discovery camp, in whose company we find
Plato, and our contemporary mathematician,
Roger Penrose.
References:
- Eric W. Weisstein, "Euler Brick," from MathWorld--A Wolfram Web Resource.
- Ivars Peterson, "Euler Bricks and Perfect Polyhedra," from Ivars Peterson's MathTrek (October 25, 1999), archived at The Mathematical Association of America web site.
- Oliver Knill, "Treasure Hunting Perfect Euler bricks," Harvard University, February 24, 2009 (PDF File).
- 101 Primitive Pythagorean Triples, Rutgers University Mathematics Department Web Site.
Permanent Link to this article
Linked Keywords: Mathematics; mathematical; Leonhard Euler; mathematician; physicist; mechanics; astronomy; Christiaan Huygens; wave theory of light; corpuscular theory; Isaac Newton; Opticks; Basel problem; infinite series formula of pi; Wikimedia Commons; brick; Euler brick; rectangle; rectangular; cuboid; edge; diagonal; integer; Pythagorean triple; set; equation; Inkscape; The On-Line Encyclopedia of Integer Sequences™; shortest edge; intermediate edge; longest edge; brute-force search; coding; computer program; source code; arbitrary-precision arithmetic library; GNU Multiple Precision Arithmetic Library; Plato; Roger Penrose.