Guessing with Benford's Law
December 18, 2013
One technique to pique a
student's interest in an abstruse subject such as
physics is to give examples where physics applies to real life. A hundred years ago, one example might be a
pendulum's period, since
pendulum clocks were common timepieces. Today, the examples might include the process by which
electrons produce light in
mobile device displays; or, how "
physics engines" make
video games so realistic.
The best examples, however, are principles that students can apply on their own to their life situations. Students are probably more likely to
program a simple video game than manufacture an
organic light-emitting diode display, and physics engines might spark the interest of just one in a hundred students. However, one thing that all students do is take
tests.
A recent
arXiv article examines how
Benford's law might be used to advantage in making
educated guesses on
multiple choice tests.[1-2] I wrote about Benford's law in a
previous article (Nuclear Benford, July 2, 2012). Benford's law says that in most
number lists, the
digit, one, will appear as the first digit with a
frequency of about 30%, and not the "expected" 11% (see graph).
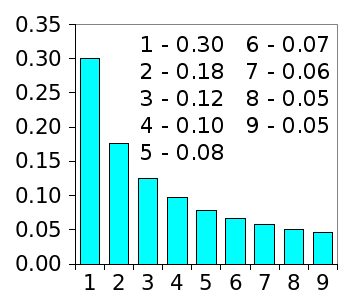
Probability that a particular digit will occupy the first place in a number.
(Graph rendered with Gnumeric)
The
probability that a particular digit will be first is given by the simple formula,
P = log10(1 + (1/n)).
The calculated percentages of a digit being in first position are as follow: 1 - 30.1%, 2 - 17.6%, 3 - 12.5%, 4 - 9.7%, 5 - 7.9%, 6 - 6.7%, 7 - 5.8%, 8 - 5.1%, and 9 - 4.6%. The law was discovered in 1881 by the
astronomer,
Simon Newcomb. Newcomb found that the earlier pages of
logarithmic tables, which were used in
multiplication and
division before computers, were most worn at the beginning, where the ones were.
Optical physicist,
Frank Benford, for whom the law is named, examined this effect in a wide variety of naturally occuring numbers in 1938. A table of his findings appears below.[3]
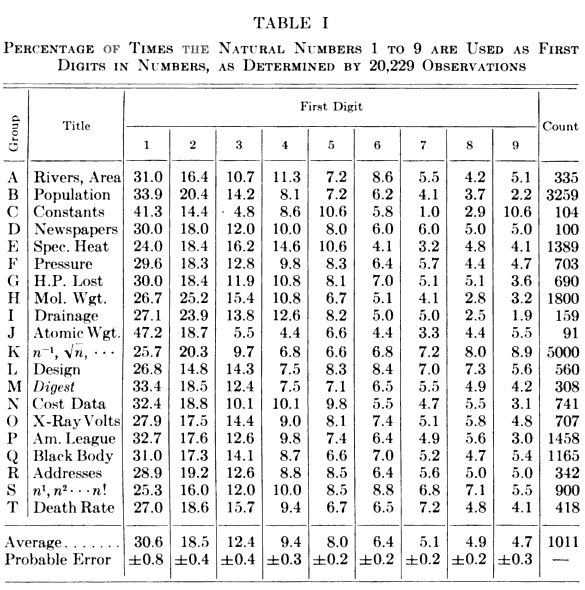
Table I from "The law of anomalous numbers," by Frank Benford, Proceedings of the American Philosophical Society, vol. 78, no. 4 (March, 1938), p. 553. (Via Google Books).[3)]
This law is not as mysterious as it seems. If you start
counting (1, 2, 3, 4, 5... etc.), there's a 100% probability of one being the first digit at
1, decreasing to 50% when you reach
2, and 11.1% when you reach
9. At that point, the probability increases to 52.6% up to nineteen, and you can see the same thing happening from 100-199, 1000-1999, etc..
Not everything in the world follows Benford's law.
Normally distributed data will not, since there's a greater expectation of numbers around the
mean of the distribution. Benford's law applies to numbers with a physical basis; namely, those that have an associated
unit, so things like
vehicle registration plate numbers,
lottery numbers, and
telephone numbers are excluded.
Mathematically-generated number lists will follow Benford's law closely. Examples are the
factorials (see graph),
Fibonacci numbers, and the
powers of numbers.
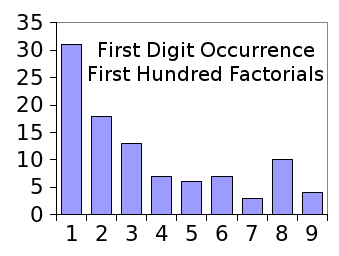
First digit occurrence in the first hundred factorials, from 0! to 99!.
Benford's law is apparent in even this small sample.
(Graph rendered with Gnumeric)
Aaron D. Slepkov and Kevin B. Ironside of the
Department of Physics and Astronomy,
Trent University (Peterborough, Ontario, Canada) and
David DiBattista of the
Department of Psychology,
Brock University (St. Catharines, Ontario, Canada) tested the
hypothesis that the answers to introductory
science textbook problems follow Benford's law.[1-2] As source material, they chose "Physics for Scientists and Engineers: A Strategic Approach" (Knight, 2013)[4], "Sears and Zemansky's University Physics" (Young & Freedman, 2000)[5], and "Fundamentals of Analytical Chemistry" (Skoog, West, and Holler, 1996).[6]
Some question answers are not numbers, or they're percentage values, so about 10-15% of the physics and 25% of the
chemistry answers did not apply. There were 3799 applicable physics answers and 294 applicable chemistry answers.[1] As can be seen from the graph, the answers indeed follow Benford's law closely.
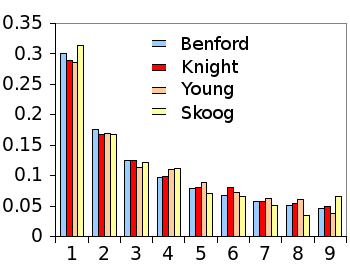
Benford's law in textbook answer sets.
(Graph rendered with data from ref. 1 using Gnumeric)[1]
The trouble from a student's point of view is that the incorrect answer choices ("distractors") also follow Benford's law.[1] Since random numbers would not, it's apparent that the distractors are not
random numbers.[1] If these textbook authors followed my approach in writing such questions, the distractors are obtained by assuming that the student multiplies where he should have divided, etc.
Benford's law offers one small advantage to students. Since correct answers with leading digits 7, 8, or 9 will appear just 15% of the time, this will help to reject some distractors when you're just guessing.[1-2]
References:
- Aaron D. Slepkov, Kevin B. Ironside and David DiBattista, "Benford's Law: Textbook Exercises and Multiple-choice Testbanks," arXiv Preprint Server, November 19, 2013.
- Benford's Law And The Art of Succeeding in Multiple Choice Tests, Technology Review, November 27, 2013.
- Frank Benford, "The law of anomalous numbers". Proceedings of the American Philosophical Society, vol. 78, no. 4 (March, 1938), pp. 551–572 (via Google Books).
- Randall D. Knight, "Physics for Scientists and Engineers: A Strategic Approach with Modern Physics (3rd Edition)," (Addison-Wesley, January 7, 2012), ISBN 978-0321740908, 1396 pp. (via Amazon).
- Hugh D. Young, Roger A. Freedman, T. R. Sandin and A. Lewis Ford, "Sears and Zemansky's University Physics (10th Edition)," (Addison-Wesley, December 6, 1999), ISBN 978-0201603224, 1274 pp. (via Amazon).
- Douglas A. Skoog, Donald M. West and F. James Holler, "Fundamentals of Analytical Chemistry (7th edition)," (Saunders College Pub., August 25, 1995), ISBN 978-0030059384, 870 pp. (via Amazon).
Permanent Link to this article
Linked Keywords: Student; physics; pendulum; period; pendulum clock; electron; OLED working principle; mobile device; physics engine; video game; computer programming; organic light-emitting diode display; assessment test; arXiv; Benford's law; educated guess; multiple choice; number; digit; frequency; probability; Gnumeric; astronomer; Simon Newcomb; mathematical table; tables of logarithms; multiplication; division; optical physicist; Frank Benford; Google Books; natural number; counting; normal distribution; normally distributed; mean; unit of measurement; vehicle registration plate; lottery; telephone number; mathematics; factorial; Fibonacci number; exponentiation; Gnumeric; Aaron D. Slepkov; Department of Physics and Astronomy; Trent University (Peterborough, Ontario, Canada); David DiBattista; Department of Psychology; Brock University (St. Catharines, Ontario, Canada); hypothesis; science; textbook; chemistry; randomness; random.