| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Nuclear Benford
July 2, 2012
Surprisingly, I've never written an article about one of the most fascinating
natural laws,
Benford's law. The law says that in most
number lists (see exceptions, below), the
digit, one, will appear with a
frequency of about 30%, and not the "expected" 11%.
This first digit law was discovered by the
astronomer,
Simon Newcomb, in 1881. In those days before
ubiquitous computing,
logarithmic tables were often used in
multiplication and
division. Newcomb found that such books were most worn at the beginning, where the ones were.
Newcomb may have discovered this law, but it's named after
optical physicist,
Frank Benford. Benford published a thorough examination of this effect in 1938. A table of his findings appears below.[1]
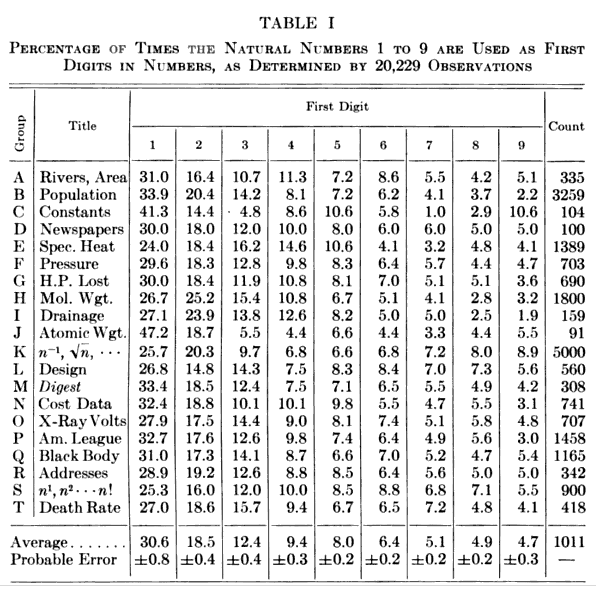
Table I from "The law of anomalous numbers," by Frank Benford, Proceedings of the American Philosophical Society, vol. 78, no. 4 (March, 1938), p. 553. (Via Google Books))
Benford's law contains predictions for the probability that other numbers will take first place. The percentages, based on an idealized statement of the law, P = log
10(1 + (1/n)), appear in the following table and graph.
| Digit | % | | Digit | % |
| 1 | 30.1 | | 6 | 6.7 |
| 2 | 17.6 | | 7 | 5.8 |
| 3 | 12.5 | | 8 | 5.1 |
| 4 | 9.7 | | 9 | 4.6 |
| 5 | 7.9 | | | |
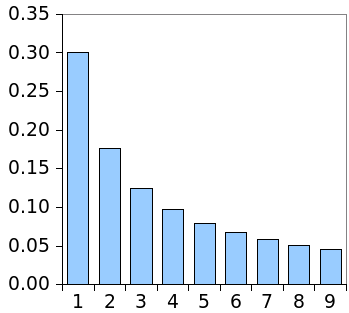
Probability that a particular digit will occupy the first place in a number.
(Graph rendered with Gnumeric)
It's easy to see how this law is possible. If you start
counting (1, 2, 3, 4, 5... etc.), you start with a 100%
probability of one being the first digit. This decreases to 50% when you reach two, and 11.1% when you reach nine. Then, the probability increases to 52.6% up to nineteen. This behavior continues with larger numbers.
The best explanation of Benford's law is
scale invariance. We measure things in nature with a particular
yardstick, but the yardstick can be divided into
inches,
centimeters, or some other unit. No matter what the unit is, the
distribution of our data points won't change. The only thing that changes is how we look at them. The only distribution that has such a property is the logarithmic distribution expressed by Benford's law.
Some datasets do not follow Benford's law. It's easy to see that
normally distributed data, such as
IQ scores, will not. In IQ scores, one as a first digit should occur about half the time, with 9 and 8 having a much higher probability than their Benford values, and 2, 3 and 4 having a first digit probability of about zero.
One interesting use of Benford's law is for
forensic accounting. If someone is "
cooking the books," their data entries would likely be
random, and they won't obey Benford's law. However, in this modern age, a competent
crook would likely program a
spreadsheet to generate numbers with a Benford distribution.
Not surprisingly,
mathematically-generated number lists, such as the
powers of numbers, the
Fibonacci numbers, and
factorials, fit Benford's law quite exactly. One interesting thing about the table in Benford's paper is the entry for "X-ray Volts," which is presumably the
voltage needed to excite the various
X-ray lines in the
elements (his text doesn't explain this). It can be seen that this
quantum process follows Benford's law quite closely.
Physicists have found that many
nuclear processes follow Benford's law.[2-6] It was found that the
half-life of 2059
β-decays demonstrate Benford's law.[2] An analysis of the half-life of 2298 nuclear decays by all modes, including
α-decay, follows the law quite closely, as shown in the figure.[3-4] The authors of the study state, however, that this is just an interesting result that gives no insight into the mechanism of nuclear decay.
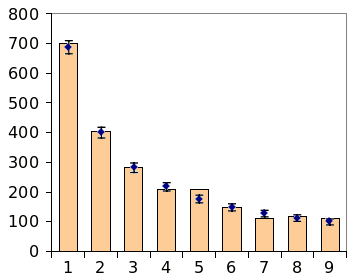
Benford's law for 2298 nuclear decay half-lives, using data from refs. 3-4.
The columns show the data, and the error bars correspond to what would be expected from Benford's law for the sample size.
(Graph rendered with Gnumeric)
References:
- Frank Benford, "The law of anomalous numbers". Proceedings of the American Philosophical Society, vol. 78, no. 4 (March, 1938), pp. 551–572 (via Google Books).
- Dong-Dong Ni, Lai Wei and Zhong-Zhou Ren, "Nuclear Physics: Benford's Law and β-Decay Half-Lives," Communications in Theoretical Physics, vol. 51, no. 4 (April, 2009), pp. 713-716.
- Janos Farkas and Gyorgy Gyurky, "The significance of using the Newcomb-Benford law as a test of nuclear half-life calculations," arXiv Preprint Server, June 18, 2010.
- János Farkas and György Gyürky, "The Significance Of Using The Newcomb–Benford Law As A Test Of Nuclear Half-Life Calculations," Acta Physica Polonica B, vol. 41, no. 6 (June, 2010), pp. 1213-1221.
- B. Buck, A.C. Merchant and S.M. Perez, "An Illustration of Benford's first digit law using alpha decay half lives, Eur. J. Phys., vol. 14, no. 2 (March, 1993), pp. 59-63); PDF copy available, here.
- Charles G. Wohl, "Benford's Law"
Permanent Link to this article
Linked Keywords: Physical law; natural law; Benford's law; number; digit; frequency; astronomer; Simon Newcomb; ubiquitous computing; logarithmic tables; multiplication; division; optical physicist; Frank Benford; Google Books; probability; Gnumeric; counting; scale invariance; yardstick; inch; centimeter; distribution; normal distribution; normally distributed; intelligence quotient; IQ score; forensic accounting; cooking the books; randomness; random; criminal; crook; spreadsheet; mathematics; mathematically-generatedvexponentiation; powers of numbers; Fibonacci numbers; factorial; voltage; X-ray spectroscopy; X-ray lines; chemical element; quantum mechanics; physicist; nuclear; half-life; β-decay; α-decay; error bar.