| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Crumpling
August 27, 2012
I'm often surprised by the quantity of items that arrive in my (
snail mail)
mailbox. Along with the usual aggregate of
bills, there's a stream of
coupons,
postcard advertisements,
tabloids of
supermarket specials, and
catalogs. The
Internet has only slightly diminished this steam of
paper, and there are forces at work to that perpetuate its existence.
My supermarket will only accept printed coupons, and not coupons presented on a
smartphone. Most of the reduction in my mail has come from my getting content online, rather than through
trade magazines; and using online search, rather than electronic component catalogs.
The interesting thing about all this is that I never really notice the paper. All my attention is directed to what's printed on it.
Marshall McLuhan may have famously stated that "
the medium is the message," but this is a
counterexample. However, the true McLuhanite might say that the
medium does play a part, since the paper coupons are sized to fit my pocket, and the tabloids unfold to a larger size that takes control of our entire
field of vision.
There's a lot of
physics in a sheet of paper, especially when it's crumpled. I wrote about crumpling in two previous articles (
Crumpled Paper, October 25, 2011, and
Paper Chase, September 7, 2010.
Physicists started to investigate crumpling of sheets of paper and other
materials about a decade ago, and they found some
universal laws.
In the mid-1990s,
Eric M. Kramer and
Alexander E. Lobkovsky of the
James Franck Institute and the
Department of Physics of the
University of Chicago recorded the emitted sound during crumpling of crumpled
Mylar sheets. When analyzed in small time slices, the acoustic emission is a series of discrete clicks.[1-2]
Sound amplitude is related to
energy, and these
experiments showed that the energies of the clicks were distributed according to a
power law distribution.
P(E) ∼ e-α
where P(E) is the probability of a click having energy E, and α is about one. The power law didn't change when the sheet material or size of the sheet was changed, so it's a universal law. The Chicago experiments showed the validity of this law over six
orders of magnitude.[3]
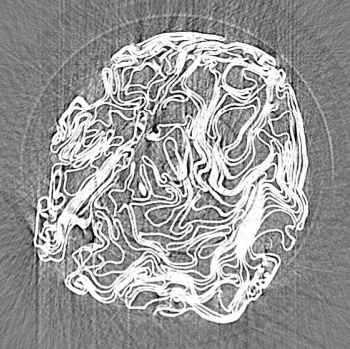
X-ray tomograph section of a compressed aluminum foil ball.
This image was constructed from a thousand projections for a ball for which the radius was compressed by a factor of six.
(Fig. 1 of ref. 4, via arXiv Preprint Server).[4-5)]
Crumpled sheets have interesting
mechanical properties, as well. A typical crumpled ball of paper may be 75% air, but it's
mechanically stiff, and quite a bit of
force is needed to crumple it further. Crumpling a sheet that's eight times larger on a side than another sheet requires only twice as much energy, although the larger sheet has sixty four times the
area of the smaller sheet. Information like this is useful if your aim is to absorb energy, as in the design of
crumple zones in an automobile.
For other interesting examples, see the references.[6-8]
One thing all these experiments have in common is the
random nature of the crumpling. Whenever possible,
experimentalists want to take more control of their experiments. That's why
physicists at the
University of Massachusetts Amherst designed an apparatus that allows crumpling of ultra-thin
polymer sheets (a few tens of
nanometers thick).[9-12] One motivation was to provide confirmatory evidence for a crumpling model they had developed with colleagues at the
Université Pierre et Marie Curie (Paris),
Oxford University (Oxford, UK), and the
Universidad de Santiago (Santiago, Chile). Although the
theory of
buckling of
compressed plates was developed by
Euler hundreds of years ago, this theory seems to deviate from experiment for very thin films.[13]
Their experiments involved placing circular disks of the thin polymer over a
water-filled orifice. Surface tension holds the film in place as applied
pressure causes a water dome to form under it, thereby crumpling the film (see figure)
A thin polymer sheet floating on a drop of water. The sheet is pulled taut from the edge of the drop orifice.
(Amherst University Image))
Before there's crumpling, there's wrinkling. The difference between these two phenomenon is the shape of the surface. There are smooth curves for wrinkling, and reentrant curves for crumpling, as can be seen in the Xray topograph, above. When the wrinkling encompasses half the sheet radius, there's a transition to crumpling that's material-independent.[11] Said
Benny Davidovitch, one of the authors of the study,
When the radius of the drop gets small enough, the thin film starts to develop fine radial wrinkles near its outer perimeter as the water pressure increases. If you keep adding pressure, decreasing the radius further, a second transition takes place and the film starts to crumple and to look more like a table cloth, draping with sharp creases over the edge of a flattened top."[9]
The basis of the theory that describes this process is that the films deform in a way that reduces the compression.[9] Wrinkling is the first feature that reduces the compression, and then there's a continuous transition to a crumpled state.[11] Of course, one of the joys of experiment is that you often discover something new along with what you expected to find. The Amherst team is looking at the finer details of the crumpled features in their experiment.[9]
References:
- Alexander E. Lobkovsky and T. A. Witten, "Properties of ridges in elastic membranes," Phys. Rev. E, vol. 55 (1997), pp. 1577-1589.
- Ivars Peterson, "Deciphering the Wrinkles of Crumpled Sheets," Ivars Peterson's MathTrek (Mathematical Association of America, May 26, 2003).
- Eric M. Kramer and Alexander E. Lobkovsky, "Universal power law in the noise from a crumpled elastic sheet." Phys. Rev. E, vol. 53 (1996), pp. 1465-1469.
- Yen-Chih Lin, Ji-Ming Sun, H. W. Yang, Yeukuang Hwu, C. L. Wang and Tzay-Ming Hong, "X-ray tomography of a crumpled plastoelastic thin sheet," arXiv Preprint Server, December 18, 2009.
- Yen-Chih Lin, Ji-Ming Sun, H. W. Yang, Yeukuang Hwu, C. L. Wang and Tzay-Ming Hong, "X-ray tomography of a crumpled plastoelastic thin sheet," Phys. Rev. E, vol. 80, no. 6 (December 16, 2009), Document No.066114 (6 pages).
- Johanna L. Miller, "What's inside a crumpled ball?" Physics Today, vol. 64, no. 10 (October, 2011), p.15.
- Anne Dominique Cambou and Narayanan Menon, "Three-dimensional structure of a sheet crumpled into a ball," Proc. Natl. Acad. Sci., vol. 108, no. 36 (September 6, 2011), pp. 14741-14745.
- Michael Marder, Robert D. Deegan and Eran Sharon, "Crumpling, buckling, and cracking: Elasticity of thin sheets," Physics Today, vol. 60, no. 2 (February 2007), pp. 33-38.
- Janet Lathrop, "UMass Amherst Physicists Discover Mechanisms of Wrinkle and Crumple Formation," University of Massachusetts Amherst Press Release, June 11, 2012.
- B. Davidov, "A sheet on a drop presents: wrinkle-to-crumple transition," University of Massachusetts Amherst Web Site, May 16, 2012.
- Hunter King, Robert D. Schroll, Benny Davidovitch and Narayanan Menon, "Elastic sheet on a liquid drop reveals wrinkling and crumpling as distinct symmetry-breaking instabilities, Proc. Natl. Acad. Sci., vol. 109, no. 25 (June 19, 2012), pp. 9716-9720.
- Supporting information for previous reference
- Benny Davidovitch, Robert D. Schroll, Dominic Vella, Mokhtar Adda-Bedia and Enrique A. Cerda, "Prototypical model for tensional wrinkling in thin sheets," Proc. Natl. Acad. Sci., vol. 108, no. 45 (November 8, 2011), pp.18227-18232.
- B. Davidov, "Understanding Wrinkling," University of Massachusetts Amherst Web Site, February 3, 2012.
- T. Witten, Forced Crumpling Web Site at the University of Chicago.
Permanent Link to this article
Linked Keywords: Snail mail; mailbox; bill; coupon; postcard; advertisement; tabloid; supermarket; catalog; Internet; paper; smartphone; trade magazine; Marshall McLuhan; the medium is the message; counterexample; medium; field of vision; physics; physicist; material; universal law; Eric M. Kramer; Alexander E. Lobkovsky; James Franck Institute; Department of Physics; University of Chicago; BoPET; Mylar; sound amplitude; energy; experiment; power law distribution; orders of magnitude; X-ray tomograph; aluminum foil; arXiv Preprint Server; mechanics; mechanical property; mechanically stiff; force; area; crumple zone; randomness; random nature; experimentalist; University of Massachusetts Amherst; polymer; nanometer; Université Pierre et Marie Curie (Paris); Oxford University (Oxford, UK); Universidad de Santiago (Santiago, Chile; theory; buckling; compression; Leonhard Euler; water; nozzle; orifice; surface tension; pressure; Benny Davidovitch.