Tikalon Blog by Dev Gualtieri

Tikalon Blog is now in archive mode. An easily printed and saved version of this article, and a link to a directory of all articles, can be found below:

This article

Directory of all articles

Arctangent Diophantine Equations

April 9, 2012

The natural numbers, which are the counting numbers (one, two, three... and first, second, third...), are really useful things. The number, 0.25, can be expressed as 1/4; or, 2/10 + 5/100. You can see that any real number can be expressed in this way, although some numbers will be harder to express than others, and pi will take a little time.

The mathematician, Leopold Kronecker was a fan of the natural numbers. Kronecker said, "God made the integers, all the rest is the work of man." This is a mathematical version of Einstein's statement that God doesn't play dice.

There are equations called Diophantine equations that require integer solutions. I mentioned Diophantine equations in a previous article (The Lonely Runner Conjecture, August 11, 2011). The need for integer solutions to certain problems is illustrated by the cattle problem, a Diophantine problem supposedly communicated by Archimedes to his friend, Eratosthenes. You wouldn't expect a fractional cow to be grazing on the plain. A spherical cow might be a special case.

A recent article on the arXiv Preprint Server examines some trigonometric Diophantine equations.[1] This paper, by Konstantine Zelator, a mathematician at Bloomsburg University of Pennsylvania, examines equations similar to the following:

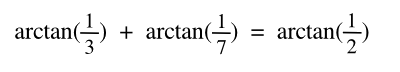(Eq. 1)

There's apparently a geometrical proof of this particular equation in a published paper, but the paper is not freely accessible online.[2] As a firm believer of the "information wants to be free" principle, I've done my own proof. The geometrical construction for the proof is shown below.

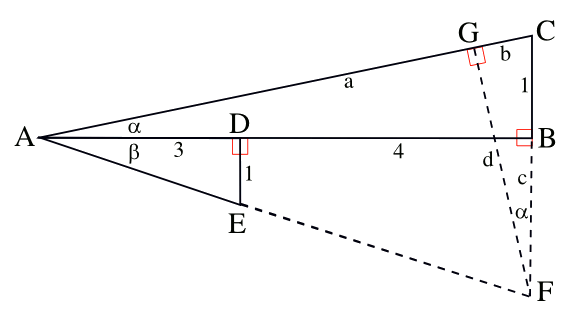
Geometrical construction to prove that arctan(1/3) + arctan(1/7) = arctan(1/2). (Rendered by the author using Inkscape)

The arctan(1/7) and arctan(1/3) triangles are ABC and ADE. Since you need a triangle that's the sum of the angles, you obviously join the triangles together, as shown. To get the tangent of the summed angle, you need to construct another right triangle, AFG, as shown. The triangle ADE is similar to the triangle ABF, and the triangle CFG is similar to triangle ABC. That knowledge, application of the Pythagorean theorem, and a lot of calculation, proves the equation.

Although a high school student would disagree, I find geometry to be fun. What I don't like is calculation, so I resort to computer models, instead. The general form of Eq. 1, shown as Eq. 2, has many integer solutions. I've written a computer program to find them, and some of these are shown in the table. The source code can be found here. The one caveat, however, is that my equations are certain only within the limits of the arithmetical precision. Since I checked the results using Gnumeric, this is about one part in 10¹⁶, but it isn't mathematical certainty.

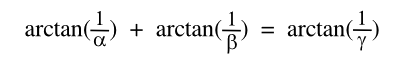(Eq. 2)

α	β	γ	_	α	β	γ
2	3	1	_	15	98	13
3	7	2	_	17	41	12
4	13	3	_	18	47	13
5	8	3	_	22	75	17
5	21	4	_	23	30	13
6	31	5	_	23	83	18
7	18	5	_	27	46	17
7	43	6	_	31	43	18
8	57	7	_	33	76	23
9	32	7	_	34	55	21
9	73	8	_	38	47	21
10	91	9	_	47	83	30
11	50	9	_	57	68	31
12	17	7	_	57	73	32
13	4	3	_	70	99	41
13	21	8	_	80	93	43
13	72	11	_	83	23	18

The fractions, 1/α, 1/β and 1/γ, needn't have just 1 as a numerator. Zelator offers Eq. 3 as an example. My computer offers Eq. 4, and many others.

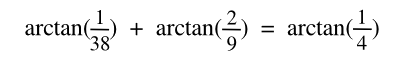	(Eq. 3)
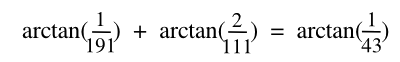	(Eq. 4)

References:

Permanent Link to this article

Linked Keywords: Natural numbers; real number; pi; mathematician; Leopold Kronecker; God made the integers, all the rest is the work of man; Einstein; God doesn't play dice; Diophantine equation; integer; Archimedes cattle problem; Archimedes; Eratosthenes; cattle; cow; spherical cow; arXiv Preprint Server; trigonometry; trigonometric; Bloomsburg University of Pennsylvania; equation; geometry; geometrical; proof; information wants to be free; Inkscape; triangle; angle; tangent; right triangle; similar triangles; Pythagorean theorem; high school student; computer model; source code; arctan.c; arithmetical precision; Gnumeric; Q.E.D.; mathematical certainty; fraction; numerator.

Latest Books by Dev Gualtieri
Previews Available
at Tikalon Press

STEM-themed novel for middle-school students

Mathematics-themed novel for middle-school students

Complete texts of LGM, Mother Wode, and The Alchemists of Mars

Other Books

α	β	γ	_	α	β	γ
2	3	1	_	15	98	13
3	7	2	_	17	41	12
4	13	3	_	18	47	13
5	8	3	_	22	75	17
5	21	4	_	23	30	13
6	31	5	_	23	83	18
7	18	5	_	27	46	17
7	43	6	_	31	43	18
8	57	7	_	33	76	23
9	32	7	_	34	55	21
9	73	8	_	38	47	21
10	91	9	_	47	83	30
11	50	9	_	57	68	31
12	17	7	_	57	73	32
13	4	3	_	70	99	41
13	21	8	_	80	93	43
13	72	11	_	83	23	18

α	β	γ	_	α	β	γ
2	3	1	_	15	98	13
3	7	2	_	17	41	12
4	13	3	_	18	47	13
5	8	3	_	22	75	17
5	21	4	_	23	30	13
6	31	5	_	23	83	18
7	18	5	_	27	46	17
7	43	6	_	31	43	18
8	57	7	_	33	76	23
9	32	7	_	34	55	21
9	73	8	_	38	47	21
10	91	9	_	47	83	30
11	50	9	_	57	68	31
12	17	7	_	57	73	32
13	4	3	_	70	99	41
13	21	8	_	80	93	43
13	72	11	_	83	23	18

α	β	γ	_	α	β	γ
2	3	1	_	15	98	13
3	7	2	_	17	41	12
4	13	3	_	18	47	13
5	8	3	_	22	75	17
5	21	4	_	23	30	13
6	31	5	_	23	83	18
7	18	5	_	27	46	17
7	43	6	_	31	43	18
8	57	7	_	33	76	23
9	32	7	_	34	55	21
9	73	8	_	38	47	21
10	91	9	_	47	83	30
11	50	9	_	57	68	31
12	17	7	_	57	73	32
13	4	3	_	70	99	41
13	21	8	_	80	93	43
13	72	11	_	83	23	18