| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Smith Numbers
May 9, 2012
Mathematicians work with
numbers like
artists work with
paint. Sometimes the numbers are regular, like a
Josef Albers' painting. Sometimes they're as
chaotic as a painting by
Jackson Pollock. Sometimes they're just playful, as in the examples that I give below.
One playfully constructed number is
Champernowne's number, sometimes called Champernowne's constant. This number is sequence
A033307 in the
The On-Line Encyclopedia of Integer Sequences, started by
Neil Sloane in 1964 when he was still a
graduate student. It's named after
D. G. Champernowne, the mathematician who published it in 1933 while he was an
undergraduate student.[1] Here are it's first few digits
0.1234567891011121314151617181920212223...
Close inspection shows that it's just the
concatenation of all the
decimal numbers, which is a very arbitrary way to form a number. Since we're doing such playful things with numbers, why stop with
base ten? Remembering that the numbers in
base two are expressed as 1, 10, 11, 100, 101, 110, 111, etc., you can build a
binary Champernowne number that looks like this,
0.11011100101110111...
A
palindrome is a word or phrase that's the same whether read forwards or backwards. One famous example of this is
Adam's supposed first words to
Eve, "Madam, I'm Adam." There are many numbers that have this same property, so writing these would be no fun at all. What's more fun is finding
prime numbers with this property. These are called, appropriately, the
palindromic primes. A simple example is the number eleven; a more complex one is 17471. The palindromic primes are
integer sequence A002385.
You can look for palindromic primes in number bases other than ten. The prime number 1991 is also a palindrome when written in
hexadecimal, 7C7.
These examples use very simple rules to specify unusual numbers. We can be more creative, as
Ramanujan was, and form something like the
taxicab numbers.
G.H. Hardy mentioned in a visit to Ramanujan that he had traveled to see him in a
taxicab with the number 1729, which seemed like a dull number. Ramanujan corrected him, saying that 1729 is the smallest number expressible as the sum of two positive
cubes in two different ways.
1729 = 13 + 123 = 93 + 103
I mentioned taxicab numbers in a
previous article (Special Numbers, September 21, 2011). There's another type of number that combines some of the flavor of prime numbers with that of Champernowne's number. These are the
Smith numbers, named by the inventive mathematician, Albert Wilansky, who found that the
telephone number, 4937775, of his brother-in-law, Harold Smith, had an unusual property.
A Smith number is a
composite number for which the sum of its digits is equal to the sum of the digits in its
prime factorization.[2] Just as for palindrome primes, we're not restricted to base ten. It's important to note that we're talking about the sum of the digits of the factors, not the sum of the factors, themselves. In the case of Smith's telephone number,
4937775 = 3 x 5 x 5 x 65837 (prime factors of 4937775)
4 + 9 + 3 + 7 + 7 + 7 + 5 = 42 (sum of digits of 4937775)
3 + 5 + 5 + 6 + 5 + 8 + 3 + 7 = 42 (sum of digits of prime factors)
The Smith numbers are
integer sequence A006753. It's been proven that there are
infinitely many Smith numbers.[3] Here are the first fifty Smith numbers.
4, 22, 27, 58, 85, 94, 121, 166, 202, 265, 274, 319, 346, 355, 378, 382, 391, 438, 454, 483, 517, 526, 535, 562, 576, 588, 627, 634, 636, 645, 648, 654, 663, 666, 690, 706, 728, 729, 762, 778, 825, 852, 861, 895, 913, 915, 922, 958, 985, 1086
A
computer program to generate Smith numbers is very easy to write; so easy, in fact, that I offer my own source code,
here. As can be seen from the two following graphs, generated by my data, the Smith numbers (at least below 10,000), on average, are rather
uniformly distributed, and the gaps between Smith numbers show no apparent
pattern. It would be interesting to assess the gap between Smith numbers as a
noise source.
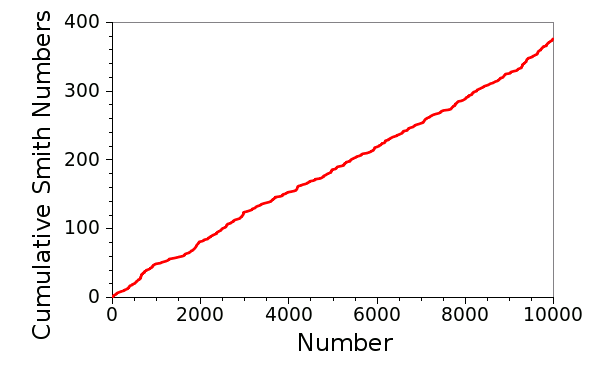
Cumulative number of smith numbers below 10,000. There are 376. (Graph rendered using Gnumeric)
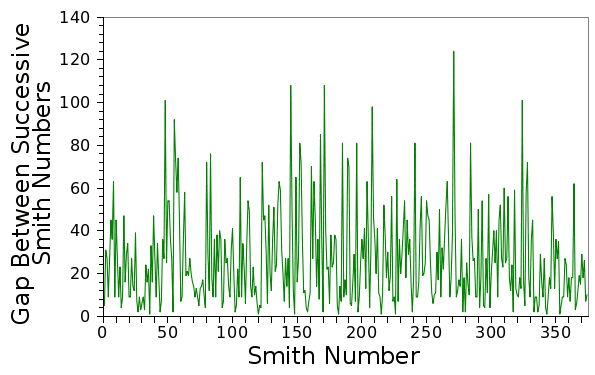
Plot of the first 375 gaps between Smith numbers. (Graph rendered using Gnumeric)
There does appear to be a predominance of small gaps, as the following
histogram of the first 375 gaps shows. Smith numbers would make an excellent topic for a
high school science fair project for those students with an affinity for computer programming. One of the first steps would be to extend source code, such as my own, to work with
big numbers.
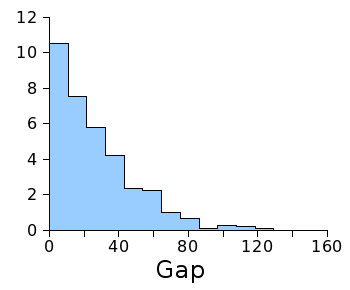
Histogram of the first 375 gaps between Smith numbers.
(Graph rendered using Gnumeric)
![]()
References:
- Eric W. Weisstein, "Champernowne Constant," From MathWorld--A Wolfram Web Resource
- Eric W. Weisstein, "Smith Number," From MathWorld--A Wolfram Web Resource.
- Wayne McDaniel, "The existence of infinitely many k-Smith numbers," Fibonacci Quarterly, vol. 25, no. 1 (February 1987), pp. 76–80.
Permanent Link to this article
Linked Keywords: Mathematician; number; artist; paint; Josef AlbersJosef Alber; Homage to the Square; painting; chaos theory; chaotic; Jackson Pollock; Champernowne's number; A033307; The On-Line Encyclopedia of Integer Sequences; Neil Sloane; graduate student; D. G. Champernowne; undergraduate student; concatenation; decimal; base ten; binary; base two; palindrome; Adam; Eve; prime number; palindromic prime; integer sequence A002385; hexadecimal; Ramanujan; taxicab number; G.H. Hardy; taxicab; cube; Smith number; telephone number; composite number; prime factorization; integer sequence A006753; infinite set; computer program; smith.c; uniform distribution; pattern; random number generation; noise source; Gnumeric; histogram; high school; science fair; gmplib.org; big numbers.