| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Sackur-Tetrode
February 2, 2012
Whenever I hear the word, "
tetrode," I think of the four-element
vacuum tube by that name. This tube has four elements (tetra-, τετρα-, is the
Greek prefix for the number four), but only if you ignore the
filament that's required to bring the
cathode to the
temperature required for
thermionic emission of
electrons. Someone who's a little younger, and more
physicist than
electrical engineer, would recall the
Sackur-Tetrode equation. The hundredth anniversary of the Sackur-Tetrode equation is this year.[1]
Vacuum tube nostalgia - A tetrode.
The elements, from top to bottom, are the plate, screen grid, control grid, cathode and filament.
Illustration by the author, rendered with Inkscape)
Otto Sackur (1880-1914) was a
German physical chemist who is known principally for this eponymous equation.
Hugo Tetrode (1895-1931) was a
Dutch theoretical physicist who hobnobbed with such luminaries as
Einstein,
Paul Ehrenfest and
Hendrik Lorentz. He published many papers on
quantum mechanics in
Zeitschrift für Physik, and other German physics
journals.
Tetrode was somewhat of a
prodigy, having published his first paper at age seventeen in the
Annalen der Physik, the preeminent physics journal of the era and the vehicle for Einstein's important papers. Like
Paul Dirac, he didn't interact well with people. He even refused a visit from Einstein and Ehrenfest when they called at his
Amsterdam residence. Tetrode died, unmarried, at the early age of thirty-five.
The Sackur-Tetrode equation wasn't a collaborative effort of Sackur and Tetrode. They developed the equation independently of each other in 1912. The equation was the first application of quantization to particle states. Until that time, only
photons were considered as
quanta, with their
energy E specified by
Planck's famous equation, E = hν, where
h is
Planck's constant and
ν is
frequency.
The quantization of photon energy handily solved some nagging problems in
electromagnetism, some of which were given interesting names, like the "
ultraviolet catastrophe." There was a similarly nagging problem in
thermodynamics involving
entropy.
Boltzmann's entropy formula, S = k ln Ω, specifies the entropy
S as a function of the number of possible states of a system,
Ω. This leads to a problem of enumerating the number of possible states of
gas molecules in a
volume.
Ludwig Boltzmann, as depicted on a 1981 Austrian stamp.
Boltzmann was a modern proponent of atomism at a time when many physicists doubted the existence of atoms. Boltzmann argued that much good physics could be done if atoms were merely supposed to exist, so no one should object to his statistical mechanics simply because of their views on atomism.
(Via Wikimedia Commons))
If
phase space were continuous, a molecule would have an
infinite space to explore. Sackur and Tetrode reasoned that the volume of phase space for a gas must be
hn, where
n is the number of
degrees of freedom. In doing so, they applied quantum theory to a statistical mechanics problem fourteen years before the 1926
Schrödinger equation. Tetrode's exposition is easier to follow than Sackur's, possibly because we've been schooled along the lines of his quantum mechanical reasoning.
Getting the math to work, and convincing others that your equation is an actual representation of reality, are two different things.
Walter Grimus, a physicist at the
University of Vienna, and author of a paper on the equation in recognition of its hundredth anniversary, writes that it was important that both Sackur and Tetrode showed the concurrence of their equation with
experimental data. They used thermodynamic data for
mercury, the
vapor of which is
monoatomic and a good approximation to an
ideal gas.[1]
To make the connection to entropy, Sackur and Tetrode needed quite a bit of data. They needed as a function of temperature the
vapor pressure of mercury, the
latent heat of vaporization, and
heat capacity of its
solid phase. Fortunately, such data were available in the published literature. In his paper, Grimus shows that a calculation of Planck's constant using the equation and modern values of the mercury data gives a result accurate to a percent.[1]
As for the equation itself, I'm leaving it in a footnote.[2] It's too complicated to explain in such a short article, so I'm following the advice of
Stephen Hawking's editor for his first popular book,
A Brief History of Time, that every equation halves the number of readers. Hawking did include one equation in this book, E = mc
2, which is as much a cultural icon as an equation.
Sackur is known principally for this equation, since he died at the young age of 34, just two years after its publication. Sackur died in an explosion in
Fritz Haber's laboratory.[1]
References:
- W. Grimus, "On the 100th anniversary of the Sackur-Tetrode equation," arXiv Preprint Server, December 16, 2011.
- The Sackur-Tetrode equation (Eq. 9 of Ref. 1, via the arXiv Preprint Server)
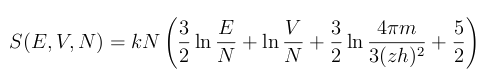
Permanent Link to this article
Linked Keywords: Tetrode; vacuum tube; Greek; filament; cathode; temperature; thermionic emission; electron; physicist; electrical engineer; Sackur-Tetrode equation; plate; screen grid; control grid; ; Inkscape; Otto Sackur; German; physical chemist; Hugo Tetrode; Dutch; theoretical physicist; Einstein; Paul Ehrenfest; Hendrik Lorentz; quantum mechanics; Zeitschrift für Physik; journal; prodigy; Annalen der Physik; Paul Dirac; Amsterdam; photon; quantum; energy; Planck's famous equation; Planck's constant; frequency; electromagnetism; ultraviolet catastrophe; thermodynamics; entropy; Ludwig Boltzmann; entropy formula; gas molecule; volume; Austrian; atomism; physicist; physics; statistical mechanics; Wikimedia Commons; phase space; infinite; degrees of freedom; Schrödinger equation; Walter Grimus; University of Vienna; experiment; mercury; vapor; monoatomic; ideal gas; vapor pressure; latent heat of vaporization; heat capacity; solid phase; Stephen Hawking; A Brief History of Time; Fritz Haber; laboratory; arXiv Preprint Server.