Newton's Gravitational Theorem
March 5, 2012
This article isn't a review of
Isaac Newton's law of universal gravitation, although that would be a worthy topic. It's the exposition of an idea that Newton first believed to be just an approximation for calculation of the
gravitational attraction between bodies that he subsequently proved as a
theorem in his
Principia.
Newton's theorem (Principia, Proposition LXXI, Theorem XXXI) is that a uniform
spherical body, as far as
gravity is concerned, can be replaced by a point
mass at its center. The concept is so ingrained into the
physics psyche that we never give it much thought. In Newton's own words,[1]
"The same things supposed as above, I say, that a corpuscle placed without the sphaerical superficies is attracted towards the centre of the
sphere with a force reciprocally proportional to the square of its distance from that centre."
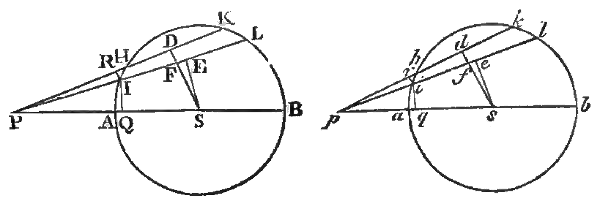
Figure from Proposition LXXI of Newton's Principia. (Click to view entire proposition.)[1)]
This is easily proved using
calculus, a
mathematics that was developed independently by Newton and
Gottfried Leibniz, Leibniz developing calculus through
integration, and Newton through
differentiation. Whereas Leibniz published his calculus, Newton kept his secret, using it to advantage in solving problems that none others could.
Infinitesimals, the stuff of calculus, were not considered to be a genuine mathematical construction in Newton's time. He would present
geometrical arguments, instead, such as for the proof of this theorem.
Since Newton's published proof is archaic, and it doesn't use calculus, it's generally unknown in the present day.
Christoph Schmid of the
Institute for Theoretical Physics of the
Eidgenoessische Technische Hochschule (ETH-Zurich, Switzerland) has published a paper on the
arXiv preprint server that reviews this theorem, which was essential to proving the
inverse-square law.[2]
Since Newton's geometrical proof is not that accessible, Schmid presents an elementary geometric proof that's easier than the use of calculus. I enjoyed my calculus courses, but I don't use calculus that often. However, one thing that I do often is write
computer simulations, which are the
last refuge of the physicist who forgot most of his mathematics.
I decided to tackle Newton's problem with a simulation program. The source code can be found,
here. The calculation, as illustrated in the figure, is quite simple. We average many values of the inverse square of the distance between a measurement point and many
random points in the interior of a sphere.
The only trick here is that we're measuring the
resolved force at the center of the sphere, so we need to multiply our values by the
cosine of the angle between our random
vectors and the vector pointing to the center of the sphere. This is easy to do by using the
dot product.
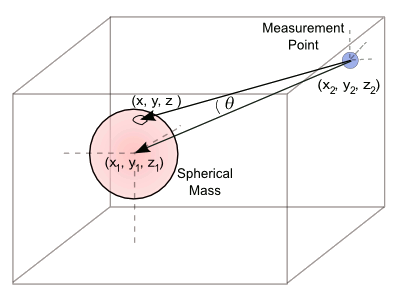
The computer simulation averages the resolved inverse-square force between a measurement point and many random points inside a sphere.
Drawing by the author, rendered with Inkscape)
The nice thing about fast
computers is that the ten million random measurements done by my program are done very quickly. The force calculation using the sphere center gives 1.20846, in arbitrary units, for my particular sphere and measurement point locations.
The computer simulation yields a force of 1.20841, or a difference of just 41
ppm (0.004%). I'm quite convinced. This is about a five and a half
sigma agreement. Perhaps a hundred million iterations would bring us to the magical
six sigma realm.

Developers of calculus, Gottfried Leibniz and Isaac Newton. Source images, left, Gottfried Wilhelm Leibniz, portrait by Christoph Bernhard Francke, c. 1700, and right, Isaac Newton, portrait by Sir Godfrey Kneller, 1689)
References:
- Isaac Newton, " Principia : The Mathematical Principles Of Natural Philosophy," English translation, via Archive.org.
- Christoph Schmid, "Newton's superb theorem: An elementary geometric proof," arXiv Preprint Server, January 31, 2012.
Permanent Link to this article
Linked Keywords: Isaac Newton; law of universal gravitation; gravitational attraction; theorem; Principia; spherical; gravity; mass; physics; psyche; Proposition LXXI; calculus; mathematics; Gottfried Leibniz; integration; differentiation; Infinitesimal; geometrical; Christoph Schmid; Institute for Theoretical Physics; Eidgenoessische Technische Hochschule (ETH-Zurich, Switzerland); arXiv preprint server; inverse-square law; computer simulation; Samuel Johnson; Patriotism is the last refuge of a scoundrel; last refuge of the physicist; Newton_gravitation.c; random; cosine; vector; dot product; Inkscape; computer; ppm; standard deviation; sigma; six sigma; Wikimedia Commons.