Planetary System Formation
March 21, 2012
Scientists continually try to make sense of their
experimental and
observational data and to
generalize what they see to a broader scope of
nature. They've found that
mathematics is a wonderful tool to do this. It works so well that
Eugene Wigner was inspired to write a paper entitled, "
The Unreasonable Effectiveness of Mathematics in the Natural Sciences."[1]
Galileo, who is known as the father of modern
physics, was among the first to apply mathematics to experimental data, and one of the first to believe that nature obeys mathematical laws. He expressed this belief in
The Assayer:
"Philosophy is written in this grand book — I mean the universe — which stands continually open to our gaze, but it cannot be understood unless one first learns to comprehend the language in which it is written. It is written in the language of mathematics, and its characters are triangles, circles, and other geometric figures, without which it is humanly impossible to understand a single word of it; without these, one is wandering about in a dark labyrinth."[2]
Johannes Kepler is known as much for the
Kepler conjecture, that the
face-centered cubic packing of
spheres is the most efficient at filling space, as his
astronomy. Having such
geometry on his mind would explain his model of the spacing of the
planets in the solar system shown in the figure.
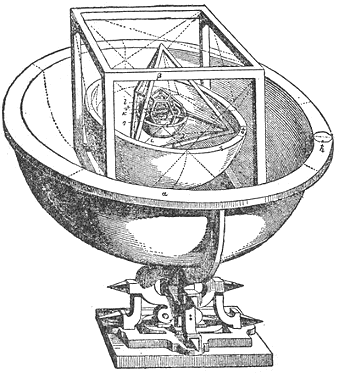
An illustration of Kepler's planetary model, as it appears in the 1910 book by Francis Rolt-Wheeler, "The Science-History of the Universe," as figure 37 on page 112.
(Scan by Sue Clark, via Wikimedia Commons))
This figure, which appears in his 1596 book,
Mysterium Cosmographicum, has a nesting of
regular polyhedra with
Saturn, the farthest known planet at his time, exists at a distance set by a sphere circumscribed around an outer
cube. The orbits of the other planets are represented by inner circumscribed and inscribed spheres. I haven't found a reference to how well these distances scale with their actual values, but someone with enough interest can easily do the calculations themselves.
A more mathematical model of planetary distance from the Sun is the
Titius-Bode Law that dates to the
eighteenth century. This law, which expresses the distance of the planets from the Sun
a in
astronomical units, is given as,
a = 0.4 + 0.3(2n), n = -∞, 0, 1, 2, 3...
As the graph shows, the equation quite well matched the distances to the planets known at the time.
Ceres was included in the law, since it seemed to fit, and it stood as a placeholder for the entire
asteroid belt. The asteroids would have formed a planet were it not for the
gravitational effects of
Jupiter.
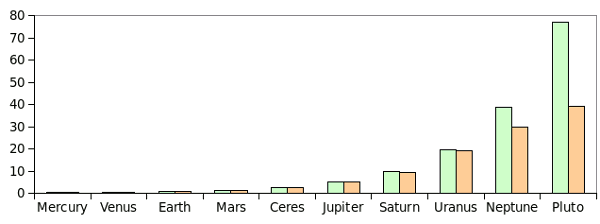
Actual distances (orange), and distances predicted by the Titius-Bode Law (green), for the planets. In this case, Ceres and Pluto are considered planets. (Rendered by author using Gnumeric)
The discovery of
Neptune in 1846 ended Titius-Bode Law's reign of accuracy. When
Pluto was discovered in 1930, the deviation from the formula was nearly 100%. Of course, there was no physical explanation as to why the law should be true, so it's just an example of
scientific numerology.
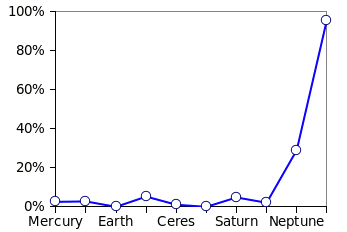
Deviation from Bode's Law.
(Rendered by author using Gnumeric)
Nowadays, with continued discovery of
exoplanets, we have more than our solitary
solar system to study. Observations of planets in orbit around
young stars have shown "planet pileups," in which many planets orbit very near to each other; and "planet deserts" that contain no planets in a wide swath of a stellar system. An explanation for this finding is contained in a paper scheduled for the
Monthly Notices of the Royal Astronomical Society and appearing as an
arXiv preprint.[3-4]
This paper, and a companion presentation at the
43rd Lunar and Planetary Science Conference by
Ilaria Pascucci of the
University of Arizona Lunar and Planetary Laboratory and
Richard Alexander of the
Department of Physics & Astronomy,
University of Leicester, describes
computer simulations of planetary formation and evolution in such systems.[3-4]
What the simulations show is that there is a competition in these systems between gravity and a process, called photo-evaporation, by which
protoplanetary material is
evaporated by the star's intense
radiation and is lost into space. Says coauthor, Alexander, "The disk material that is very close to the star is very hot, but it is held in place by the star's strong gravity... Further out in the disk where gravity is much weaker, the heated gas evaporates into space."[3] Somewhat further out, there isn't enough radiation for evaporation.
For such stars a gap results from these competing processes at a distance of about 1-2 astronomical units. As explained by coauthor, Pascucci, "The planets either stop right before or behind the gap, creating a pile-up... The local concentration of planets leaves behind regions elsewhere in the disk that are devoid of any planets. This uneven distribution is exactly what we see in many newly discovered solar systems."[3]
Their research was funded by the
US National Science Foundation and the
UK Science and Technology Facilities Council.[3]

Artist's conception of a protoplanetary disk around the brown dwarf, OTS 44.
(Image: NASA Spitzer Space Telescope Collection, NASA/JPL-Caltech/T. Pyle))
![]()
References:
- E.P. Wigner, "The unreasonable effectiveness of mathematics in the natural sciences," Communications on Pure and Applied Mathematics, vol. 13, no. 1 (February, 1960). pp. 1-14. A PDF file is available, here.
- Galileo quotations on Wikiquotes; Selections of a translation of The Assayer; Stillman Drake, "Discoveries and Opinions of Galileo," Doubleday & Co.(New York, 1957), pp. 231-280.
- Daniel Stolte, "Popular Solar System Orbits Result in 'Planet Pileups'," University of Arizona Press Release, March 19, 2012
- R.D. Alexander and I. Pascucci, "Deserts and pile-ups in the distribution of exoplanets due to photoevaporative disc clearing," arXiv Preprint Server, February 24, 2012.
Permanent Link to this article
Linked Keywords: Scientist; experiment; observation in science; data; theory; nature; mathematics; Eugene Wigner; The Unreasonable Effectiveness of Mathematics in the Natural Sciences; Galileo; physics; The Assayer; Johannes Kepler; Kepler conjecture; face-centered cubic; sphere; astronomy; geometry; planets; Sue Clark; Wikimedia Commons; Mysterium Cosmographicum; Platonic solid; regular polyhedra; Saturn; cube; Titius-Bode Law; eighteenth century; astronomical unit; Ceres; asteroid belt; gravitation; Jupiter; Pluto; Gnumeric; Neptune; Eddington number; scientific numerology; exoplanets; extrasolar planet; solar system; Hertzsprung-Russell diagram; young star; Monthly Notices of the Royal Astronomical Society; arXiv; preprint; 43rd Lunar and Planetary Science Conference; Ilaria Pascucci; University of Arizona; Lunar and Planetary Laboratory; Richard Alexander; Department of Physics & Astronomy; University of Leicester; computer simulations; protoplanetary; evaporation; electromagnetic radiation; US National Science Foundation; UK Science and Technology Facilities Council; NASA; Spitzer Space Telescope Collection; JPL; Caltech; T. Pyle.