| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Squaring the Circle
July 15, 2011
When I was an
elementary school student studying the "
new math," I was inspired to try my hand at a classical
geometry problem. This was the
trisection of angles; that is, dividing an angle into three equal angles using only the tools of geometry, a
straightedge and
compass. Except for special cases, such as dividing a right angle into thirty-degree angles, it's not possible. In 1837,
Pierre Wantzel showed that this problem reduces to the solution of a certain
cubic equation that does not translate to a straightedge and compass rendition.
As all parents and teachers know, the one way to get a child to do something is to tell him not to do it. So, armed with a straightedge and compass, I spent many hours in my bedroom trying procedures on random acute angles. When one of these showed promise, I would repeat it on a random obtuse angle. Well, Wantzel was right, but I got a lot of practice with geometry tools. Trisection of angles is possible using other methods.[1]
Another unsolvable problem in geometry is
squaring the circle. The problem is to construct a
square having the same area as a given
circle, again using only the tools of geometry, a straightedge and compass. You might think that it's somewhat easier to see why this task might be impossible, since the area of a circle involves pi, an
irrational number. However, the
hypotenuse of a
right triangle with unit sides is the
square-root of two, which is also irrational, so we can construct at least one irrational line segment.
The thing that makes squaring a circle impossible is not merely pi's irrationality. Pi is a
transcendental number, which was proved in 1882 in the
Lindemann–Weierstrass theorem. The transcendental nature of pi means that we can't construct a line segment that's the square-root of pi. This is required to generate a square of area equal to that of a unit circle. Squaring a circle would mean that we can find an algebraic representation of pi.
Unlike the angle trisection problem, finding the area of a circle has many applications, even when not followed by an actual construction of the equivalent square, so it's gotten much more attention. Of course, an approximate value of pi is needed to calculate the approximate area of a circle.
The
Egyptians were very concerned with area, since the
annual flooding of the Nile made
surveying of land an important occupation (How could I not mention the
Cappadocian hydrological engineers). The
Rhind papyrus (1800 BC) gives the area of a circle as (64/81)d
2, where d is the circle diameter. In this case, pi is approximated by 256/81, or about 3.16.
One common approximation for pi is (355/113), which is easily remembered by writing the first three odd numbers twice. This faction evaluates to 3.14159292..., which is quite close to the actual value of pi, 3.14159265...
Srinivasa Ramanujan gave a geometrical construction of this fraction in 1913 and he was able to square the circle to about 0.00001%, or ten parts per million.[2] As Ramanujan wrote,
"If the area of the circle be 140,000 square miles, then [the length of a side of the square] is greater than the true length by about an inch."
This, as my
building contractor father would say when surveying for the foundation of a new house, is "close enough for digging." There are more extreme examples that bring this to a better than
ppm level.
Hippocrates (of Chios) thought he was close to squaring the circle when he examined the properties of his
lune, which is shown in the figure. He showed that the area between the arcs "E" and "F" in the figure was the same as the area of triangle ABO.
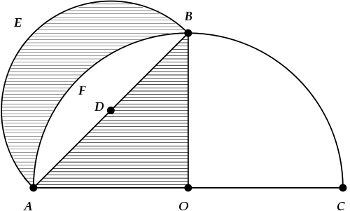
Lune of Hippocrates.
Drawing by Michael Hardy, via Wikimedia Commons)
In a paper posted recently on the
arXiv preprint server, Henryk Fukś of the
Fields Institute and the
University of Guelph, presents the
Latin original and a side-by-side English translation of a 1685 paper by the
Jesuit,
Adam Adamandy Kochański.
Kochański, who was court
mathematician and
librarian for the
King of Poland, presents some
rational approximations for pi, and a geometrical construction for a line segment approximately equal to π
2.[3] As Kochański confesses in his paper,
"For my part, I do not deny that I too was once affected by the same weakness, and, to omit other things, I put not a small effort into squaring of a circle and in examination of works of others attempting it."[4]
Would that modern scientific papers, or at least
blogs, were written in the same style!
"I must confess that it was not just for a short period that my brain troubled over such a thing as Kochański's construction. Then, Lo! The darkness was lifted from my eyes, and I saw clearly the logic that flowed from his able pen."[5]
Kochański gives a construction, shown in the figure, that generates an approximation of π
2. In this figure, the angles, ∠IAC and ∠KAC, on a unit circle are sixty degrees, and the line segment HL = BD. Knowing this allows the conclusion that IL
2 = IK
2 + KL
2 = 9.869231718195572759955..., the square root of which is 3.141533339...
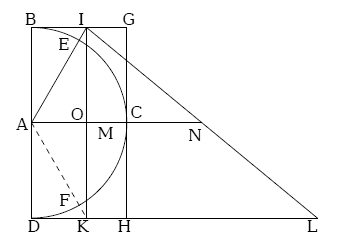
Kochański geometrical construction to approximate pi. The angles ∠IAC and ∠KAC are 60°, HL=BD, and IL is close to π2 for a unit circle.
(Via arXiv Preprint Server)[3])
![]()
References:
- Trisection of Angles page on Wikipedia.
- Srinivasa Ramanujan, "Squaring the circle," Journal of the Indian Mathematical Society, 1913, p. 132.
- Henryk Fukś, "Observationes Cyclometricae by Adam Adamandy Kochański - Latin text with annotated English translation," arXiv Preprint Server, June 9, 2011.
- Haud equidem diffiteor, me quoque olim eodem morbo laborasse, et ut alia praeteream, Circulo quidem quadrando, vel examinandis aliorum in eo conatibus, operae non nihil collocasse.
- Fateor non modo paulisper mea turbaris cerebro quid tale quod Kochańskii elit. Ecce! Tenebrae lumina pectore cessit, et vidi clare quod logica perito stylo fluebant.
Permanent Link to this article
Linked Keywords: Elementary school; new math; geometry; trisection of angles; straightedge; compass; Pierre Wantzel; cubic equation; squaring the circle; square; circle; irrational number; hypotenuse; right triangle; square-root of two; transcendental number; Lindemann–Weierstrass theorem; Egyptians; annual flooding of the Nile; surveying; Cappadocian hydrological engineers; Rhind papyrus; Srinivasa Ramanujan; building contractor; ppm; Hippocrates of Chios; lune; Wikimedia Commons; arXiv preprint server; Fields Institute; University of Guelph; Latin; Jesuit; Adam Adamandy Kochański; mathematician; librarian; King of Poland; rational number; blog.