The Lonely Runner Conjecture
August 11, 2011
When I was a
college freshman, my
dorm mates talked me into being the captain of our
intramural track team. It wasn't because I was fleet of foot. In fact, they said I wouldn't need to run at all. I would just act as a records keeper. Perhaps they admired my skill at holding a
clipboard.
What they didn't tell me was that when there was an absent runner, the captain needed to run the race. That happened once, I finished dead last, but it did teach me a valuable lesson. When you're volunteering for something, make certain you know what you're volunteering for.
There's an interesting
mathematics problem called the
lonely runner conjecture. It involves runners who start a race together on a circular track, they all run at different rates, and they're indefatigable; that is, they don't just run till they drop, they run at their constant speed and never drop. The
conjecture is that there will be times at which any given runner will be at a distance of at least a fraction (1/n) of the track length from any other runner.
There is one caveat, however. The runners' rates must be pairwise distinct; that is, all rates are different. As typical, the easiest stated conjectures turn out to be hard to
prove. Proofs are known up to seven runners, and the seven runner proof was published in 2008.[1-3]
This problem is quite easy to
simulate, so I wrote a simulation program, which can be found
here. For six runners, the following graph shows the percentage separation from the closest runner for one particular runner over 10,000 steps. The program assigns random running rates to the runners. The fastest runner in this case made a complete circuit in 109 steps, and the slowest runner completed the circuit in 304 steps. A peak separation of 37.9% occurs at 9,000 steps.
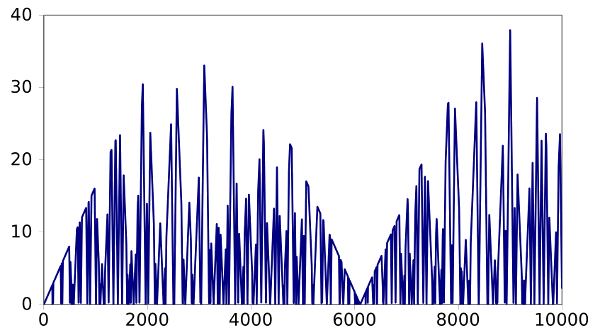
Separation from the closest runner for a particular runner over 10,000 steps in a simulation of the lonely runner conjecture. There's a peak separation of 37.9% at 9,000 steps. (Graph via Gnumeric).
The schematic of the runners' track in the figure below shows the position of the runners at 9,000 steps. There are two "cozy" runners who are separated by just 0.37% of the track length, and the one lonely runner who's 37.9% distant from the nearest runner.
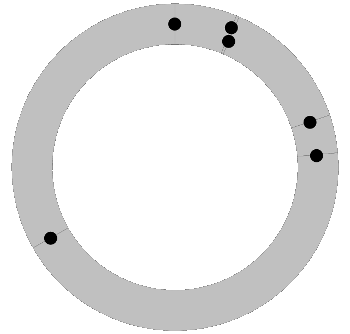
Two cozy, and one lonely runner, as calculated by the simulation program.
The runners are at 7.90%, 8.27%, 17.65%, 22.13%, 60.49% and 98.43% of the track length.
(Graph via Gnumeric))
For six runners, the lonely runner conjecture requires merely 1/6 of the track length as the distance to the nearest runner, and we see much more. Why the discrepancy? The (1/n) term is in the conjecture because it makes the problem more tractable. In that form, it can be addressed by
Diophantine approximation, which is the approximation of real numbers by rational numbers.
Whenever I see
Diophantine equations, the word,
piebald, comes to mind. After hearing a word like piebald, how could you forget the context in which you first heard it? In my case it was in the
cattle problem, a Diophantine problem supposedly communicated by
Archimedes to his friend,
Eratosthenes.[4-5] You can view the original
Greek text
here.[6]
The problem concerns the number of
cattle owned by the sun god,
Helios, some of which were white, some blue, some yellow, and some piebald. It was basically a Diophantine equation system of seven
equations in eight unknowns.
Cajori, whom I read as a student, uses the word, piebald.[4-5] Modern authors tend to use terms like dappled and spotted, but I'm a piebald man, through and through.
A paper posted recently on the
arXiv preprint server uses
Fourier analysis of the lonely runner conjecture to conclude that the separation gets very close to half the track length.[7] This makes a lot of sense, since we can imagine that by waiting long enough, all runners except one will group together, and the remaining runner will be at a random place on the rest of the track. If we're really patient, the random place of the remaining runner will be halfway around the track from the crowd of other runners. This is not a proof, but it gives us a warm feeling.
I leave you with the image of the hand of the anonymous "
Googler" who brought us the online text of Cajori's 1894 "A History of Mathematics."[5]
Image found in the online scan of
Florian Cajori, "A History of Mathematics," MacMillan Company, (New York, 1894)
References:
- Lonely runner conjecture, Open Problem Garden Web Site.
- J. Barajas and O. Serra, "The lonely runner with seven runners," arXiv Preprint Server, October 24, 2007.
- J. Barajas and O. Serra, "The lonely runner problem with seven runners," The Electronic Journal of Combinatorics, vol. 15, no. R48, pp. 111-116.
- Florian Cajori, "A History of Mathematics," MacMillan Company, (New York. 1919), Second Edition, p. 59f. (via Scribd),
- Florian Cajori, A History of Mathematics, MacMillan Company, (New York, 1894) , p. 73f. (via Google Books).
- Archimedes Cattle Problem, Greek text, New York University.
- Sebastian Czerwinski, "Random runners are very lonely," arXiv Preprint Server, February 22, 2011.
- C. Harold Horvat and Matthew Stoffregen, "A Solution to the Lonely Runner Conjecture for Almost All Points," arXiv Preprint Server, March 8, 2011.
Permanent Link to this article
Linked Keywords: College freshman; dorm; intramural; track team; clipboard; mathematics; lonely runner conjecture; conjecture; mathematical proof; computer simulation; Diophantine approximation; Diophantine equations; piebald; Archimedes cattle problem; Archimedes; Eratosthenes; Greek language; cattle; Helios; equation; Florian Cajori; arXiv preprint server; Fourier analysis; Googler; A History of Mathematics.