Lexical Distance
June 27, 2011
Science revolves around numbers. Comparing objects is much easier if they are assigned numbers. Although its early history was descriptive,
physics since the time of
Galileo has been based on numbers. After a time, the other sciences subscribed to the number concept, an idea that's sometimes called "
physics envy."
Physics Nobelist,
Eugene Wigner, summarized the concept nicely when he wrote,
"The miracle of the appropriateness of the language of mathematics for the formulation of the laws of physics is a wonderful gift which we neither understand nor deserve. We should be grateful for it and hope that it will remain valid in future research and that it will extend, for better or for worse, to our pleasure, even though perhaps also to our bafflement, to wide branches of learning."[1]
Many non-science disciplines have adopted some principles of
mathematics, since they're so useful.
Statistics, of course, is preeminent, but some researchers have applied other mathematical techniques that are common in the sciences. This is illustrated in a recent paper by
Maurizio Serva of the Dipartimento di Matematica,
Università dell'Aquila (
L'Aquila, Italy) that attempts to uncover the degree of relationship between
languages.[2] The ultimate objective of this paper, and similar papers on this topic, is the explication of language
phylogeny; that is, the evolutionary path of language and development of a language "family tree."
Comparative linguistics has been an active topic for many years, and students who have taken a foreign language course have noticed similarities between words in their native language and the one they're learning. Languages in particular language families, such as the
Romance languages, have many similar words. The common examples are words relating to "mother;" for example, we have
mater (mother) in
Latin, and the corresponding
maternal in
English. Going farther back, it seems that the "ma" vocalization has meant mother since the dawn of humanity.
The usual technique for language comparison is to examine the shared
cognates between languages, something that I wrote about in relation to the Ugaritic language in a
previous article (Ugaritic, July 16, 2010). Cognates are words in different languages that have a common
etymological origin. For example, the English, "silver," and
German, "silber;" or the Latin "argentum,"
French, "argent," and
Italian, "argento."

This might look like mathematical notation, but it's actually the word, Inuktitut, in Canadian Aboriginal syllabics.
(Via Wikimedia Commons).
Serva's paper, "Phylogeny and geometry of languages from normalized Levenshtein distance,"[2] goes beyond the cognate principle to do a quantitative analysis of languages using the the
Levenshtein distance. The Levenshtein distance is more familiar to
computer programmers than
linguists. The Levenshtein distance, or a close cousin, is the mathematical function behind the code that asks, "Did you mean...," when you type something partially, or incorrectly, into a web search box.
The Levenshtein distance is the minimum number of operations needed to transform one string into the other by deletion, insertion, or substitution of single characters.[3] A variant, developed by Damerau and known as the Damerau–Levenshtein distance, considers transposition of characters as a single operation, whereas such an operation would be doubly counted as substitutions by Levenshtein.[4]
Serva makes a reasonable modification of Levenshtein distance in his application. Changing a single letter in a short word will have a much larger affect on its meaning than changing a letter on a long word. By definition, each of these changes are assigned to same Levenshtein distance, although one of them is a much larger change, lexically speaking, than the other. Serva solves this problem by a
normalization, generating a lexical distance
d, as follows:
d(ω1,ω2) = dL(ω1,ω2)/l(ω1,ω2),
where
ω1 and
ω2 are the two words that are being compared,
dL is the Levenshtein distance, and
l is the length of the longest word of the two being compared. The normalized lexical distance will have values between zero and one.
So, what's Serva's method of language comparison? It's easily understood by computer and physical scientists. You construct a list of words with the same meaning in each language (Serva takes this number, M, to be a reasonable 200), and then do a normalized sum over all these words. For example, comparing languages α and β, the lexical distance
D between these would be
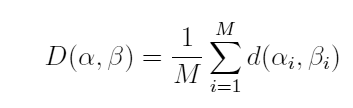
Serva applied this analysis to dialects of the
Malagasy language of
Madagascar. the closest language to Malagasy is
Maanyan, a language of
Borneo. His analysis shows that the Malagasy language originated at the south-east coast of the island and exists as a dialect called
Antandroy. The dialects that spring from Antandroy are in geographical isolation from each other.
See reference 5 for a paper of mine that mentions the Levenshtein distance.[5]
References:
- Eugene Wigner, "The Unreasonable Effectiveness Of Mathematics In The Natural Sciences," Communications in Pure and Applied Mathematics, vol. 13, no. 1 (February 1960).
- Maurizio Serva, "Phylogeny and geometry of languages from normalized Levenshtein distance," arXiv Preprint Server, April 29, 2011.
- V. I. Levenshtein, "Binary codes capable of correcting deletions, insertions, and reversals," Proceedings of the USSR Academy of Sciences, vol. 163, no. 4 (1965), pp. 845-848; Appeared in English as V. I. Levenshtein, "Binary codes capable of correcting deletions, insertions, and reversals," Soviet Physics Doklady, vol. 10 (1966), pp. 707-710.
- F.J. Damerau, "A technique for computer detection and correction of spelling errors," Communications of the ACM, vol. 7, no. 3 (March 1964), pp. 171-176.
- D.M. Gualtieri, FauxCrypt - A Method of Text Obfuscation, arXiv Preprint Server, April 28, 2010.
Permanent Link to this article
Linked Keywords: Science; physics; Galileo; physics envy; Physics Nobelist; Eugene Wigner; mathematics; statistics; Maurizio Serva; University of L'Aquila; L'Aquila, Italy; language; phylogeny; comparative linguistics; romance language; Latin; English; cognate; ugaritic; etymology; German; French; Italian; Wikimedia Commons; Levenshtein distance; computer programmer; linguist; normalization; Malagasy language; Madagascar; Maanyan; Borneo; Antandroy; "The Unreasonable Effectiveness Of Mathematics In The Natural Sciences.