Random Walks and Lévy Flights
May 19, 2011
Surprisingly, there are many more
blond jokes on the Internet than
drunkard jokes. If
clinical trials of
baclofen as a cure for
alcohol addiction are successful, there may be even fewer.[1] I'll start this article with one of my favorites.
A drunkard was under a streetlight searching on his hands and knees for something. A passerby saw his plight and offered to help.
"What are you looking for?" he asked.
"My car keys," was the reply.
After helping in the search for a few minutes and finding nothing, the passerby asked, "About where did you drop them?"
The drunkard pointed towards a car in the distance.
"Then, why are you looking here!" exclaimed the passerby.
"Because the light's better," the drunkard replied.
Because of their erratic behavior, drunkards are used as examples of
random and nearly random processes. We have the
random walk of a drunkard wandering aimlessly in a park. We also have the mostly directed walk, called a
drunkard's walk, of a more sober drunkard walking back home after a few rounds at the local tavern.
A random walk is quite easy to program. You decide on
distributions for the step size and direction, and you randomly choose each step from these distributions. Usually, a two dimensional random walk is just programmed as a
uniform distribution of x increment and y increment in a plane. Some
C code for a two dimensional random walk is
here, and the following figure shows an example.

A two dimensional random walk using data from the author's program.
Plot via Gnumeric)
There's another type of random walk that has a little intelligence behind it. A
Lévy flight, as it's called, consists of random walks interspersed by long travels to different regions of the walk space; that is, there is a long movement to a random
area, and then smaller movements at that area. Lévy flights are named after the French mathematician,
Paul Pierre Lévy. Mathematicians and electrical engineers will recognize his academic pedigree, since he was a student of
Jacques Hadamard.
In a
previous article (Lévy Flight, November 15, 2007), I discussed the possibility that
animals foraging for food might use a Lévy flight strategy. This makes a lot of sense. If you can't find any food in a particular area, it's probably best to go somewhere else. A paper published last year in
Nature provides evidence that
open-ocean predatory fish, such as
sharks,
tuna,
billfish and
ocean sunfish, forage in this way.[2-4] Evidence of such behavior for other animals is still controversial.[5-7]
Our drunkard, when thrown out of one bar, should use a Lévy flight to find his next watering hole. It wouldn't do much good to look for another bar in the same neighborhood as the one you've left, since
zoning laws typically require a minimum separation. Our drunken friend would do well to stagger a few blocks in any direction, and then do a local search. One type of Lévy flight is shown in the following figure. It was generated using the source code mentioned above.
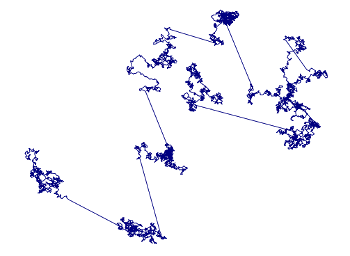
A particular type of Lévy flight using data from the author's program.
Plot via Gnumeric)
Another type of random walk is the
self-avoiding walk, which is a random walk in which you aren't allowed to cross a previously tread path. This type of walk is typically rendered on a
lattice. I tried to code it for arbitrary step and direction with limited success.
The self-avoiding walk was invented by
Paul Flory, who won the
Nobel Prize in Chemistry in 1974.[8] Its purpose is to mimic the
conformations of
polymer chains in
solution, since the guiding principle is that no two things can occupy the same space at the same time. This is one problem where
computer simulations have had more success than
mathematics.

Self avoiding walk on a square lattice.
Image by Claudio Rocchini, via Wikimedia Commons)
The works of
Jackson Pollock appear to have Lévy flight structure.[9] Refs. 10-12 contain further information on Lévy flights.[9-12]
![]()
References:
- Martin Enserink, "Anonymous Alcoholic Bankrolls Trial of Controversial Therapy," Science, vol. 332, no. 6030 (May 6, 2011), p. 653.
- Alexandra Witze, "Sharks Have Math Skills," Discovery, June 10, 2010.
- James Dacey, "Sharks hunt via Lévy flights," physicsworld.com, June 11, 2010
- Nicolas E. Humphries, Nuno Queiroz, Jennifer R. M. Dyer, Nicolas G. Pade, Michael K. Musyl, Kurt M. Schaefer, Daniel W. Fuller, Juerg M. Brunnschweiler, Thomas K. Doyle, Jonathan D. R. Houghton, Graeme C. Hays, Catherine S. Jones, Leslie R. Noble, Victoria J. Wearmouth, Emily J. Southall and David W. Sims, "Environmental context explains Lévy and Brownian movement patterns of marine predators," Nature, vol. 465, no. 7301 (June 24, 2010), pp. 1066-1069.
- G. M. Viswanathan, V. Afanasyev, S. V. Buldyrev, E. J. Murph, P. A. Prince and H. E. Stanley, "Lévy flight search patterns of wandering albatrosses," Nature, vol. 381 (30 May 1996), pp. 413-415 .
- 'Lévy Flight' Theory Of Food Foraging In Albatross Overturned, Say Researchers (News Account, October 24, 2007).
- Andrew M. Edwards, Richard A. Phillips, Nicholas W. Watkins, Mervyn P. Freeman, Eugene J. Murphy, Vsevolod Afanasyev, Sergey V. Buldyrev, M. G. E. da Luz, E. P. Raposo, H. Eugene Stanley and Gandhimohan M. Viswanathan, "Revisiting Lévy flight search patterns of wandering albatrosses, bumblebees and deer," Nature, vol. 449 (October 25, 2007), pp. 1044-1048.
- At my first scientific conference (on thermochemistry), I chatted with Maurice Huggins, who was an originator of what is called the Flory–Huggins solution theory.
- Richard P. Taylor, Adam P. Micolich and David Jonas, "Fractal expressionism," Physics World, vol. 12, no. 10 (October 1999).
- Kate Ravilious, "Locating, locating, locating," New Scientist, no. 2579 (November 25, 2006), pp.44-47.
- O. Bénichou, C. Loverdo, M. Moreau, R. Voituriez, "Intermittent search strategies," arXiv Preprint Server, April 1, 2011.
- Ihor Lubashevsky, "Truncated Lévy Random Walks and Generalized Cauchy Processes," arXiv Preprint Server, April 1, 2011.
Permanent Link to this article