A Foucault Gyroscope
February 14, 2011
One of the books on my bookshelf (a dead tree book, already twenty years old, and probably destined to last much longer than any electronic book) is
Umberto Eco's, "
Foucault's Pendulum."[1] Eco is known also for
The Name of the Rose, which became an excellent
film starring
Sean Connery[2] that few have seen. Eco is a professional
semiotician, which is a perfect starting point for writing fiction.
I learned about Eco's Foucault's Pendulum while listening to
National Public Radio (now known as NPR) on a drive back from the airport late one night after a business trip. The name of the book was easy for me to remember, since
Foucault's Pendulum is an historic artifact that demonstrated the rotation of the
Earth. The book is an unusual and entertaining mixture of topics, including
vanity publication services,
conspiracy theories,
coded messages hidden in
manuscripts,
alchemy and
ectoplasmic entities. The book takes its title from a scene in the
Musée des Arts et Métiers which contained a pendulum with
Foucault's original pendulum bob.[3]
In 1851, Foucault first demonstrated his pendulum at the
Paris Observatory, but not after doing a
proof of concept in his basement. His basement experiments were done at night, since daytime traffic added too much noise to his small, demonstration system.[4] The pendulum at the Paris Observatory had a ten meter wire, and it worked as expected. It was his massive 28 kilogram bob suspended on a 67 meter wire suspended from the from the dome of the
Paris Panthéon that captured the most attention. The plane of swing of the pendulum rotated clockwise eleven degrees per hour; that is, it made a full circle in 32.7 hours. This was the calculated response for a pendulum at the
latitude of Paris (48
o 48' N).
The reason the pendulum behaves this way is that the Earth rotates, but the pendulum maintains its motion with respect to
absolute space; or, as they said more poetically in Foucault's time, with respect to the fixed stars. Putting on our
technologist cap, we see that if we carry such a pendulum with us, we'll always know our orientation with respect to a reference point. Better yet, if we could somehow have three orthogonal versions of the pendulum, we would know our precise three dimensional orientation.
Well, pendulums on a Foucault scale are too large to carry with us, and they only swing under the influence of
Earth's gravity; so, no orthogonal pendulums for you. However, Foucault's initial experiment wasn't with a pendulum. It was with a vibrating rod. He clamped the rod in the
chuck of a
lathe, struck it to get it vibrating, and then rotated the lathe.[4] Quite surprisingly, the rod continued to vibrate in its original plane. Such a vibrating rod will work as a direction sensing device, although with not much accuracy.
That's why
gyroscopes were used for navigation before GPS, and even now in systems that can't rely on the presence of
GPS, such as
spacecraft. The mechanical gyroscope is well known to children, since it's a popular toy. Once it's set spinning, it will maintain its absolute orientation in space until the wheel runs down. A large gyroscopic mass spinning at high speed will give an accurate direction-sensing device. Navigation gyroscopes will use
magnetic or other forces to keep the wheel rotating, although there's sometimes a sphere instead of a wheel.[5]
Engineers dislike mechanical systems, since they're usually less reliable than purely electronic systems; so, the
ring laser gyroscope and its cousin, the
fiberoptic gyroscope, were invented. These work on the principle, known as the
Sagnac effect, that counter-propagating light beams around a closed path will shift in
phase under rotation. The closed path is typically a rectangle or a triangle with a mirror at each apex. Unfortunately for the purists, a mechanical component is required in the most accurate RLGs, since the counter-propagating light beams will "lock" at rotation rates near zero and cause errors. This locking is usually defeated by having one of the mirrors vibrate.
MEMs systems, although mechanical, are generally more reliable than large mechanical systems. As a consequence, there are many types of
MEMs gyroscopes. One caveat is that the most common MEMs gyroscopes don't monitor direction directly. They're
accelerometers that measure the rate of change of angle. Electronic circuitry integrate this
derivative signal to provide an absolute angle. As can be imagined, a lot of errors can creep into such an indirect system, but these sensors are useful in many applications for which long-term precision is not required.
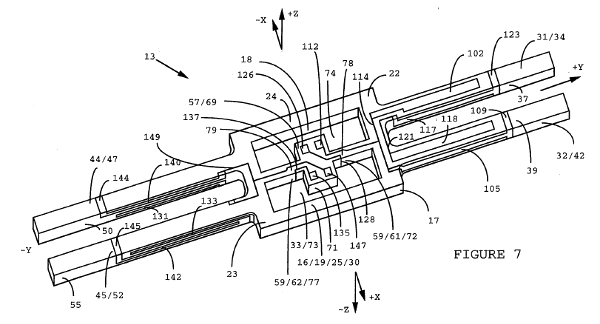
A tuning fork gyroscope. Fig. 7 of US Patent No. 5,396,144 (Piyush K. Gupta and Craig E. Jenson, "Rotation rate sensor with center mounted tuning fork," Mar 7, 1995; see Ref. 6.)
Most such MEMs gyroscopes are variants of a
tuning fork. When a tuning fork rotates, the
Coriolis forces on the vibrating tines will cause a
torsional force at the base of the tuning fork that's easy to detect. The force is proportional to the angular rate. An example of an early implementation is shown in the above figure.[6] As you can see, turning a tuning fork into a useful angular rate sensor is somewhat difficult.
What would be especially desirable is a device that gives an orientation angle directly - A Foucault pendulum on a chip.
Andrei M. Shkel, professor of mechanical and aerospace engineering at the
University of California (Irvine), patented a Foucault concept in a MEMs device in 2002.[7] Shkel and his associates at the UC Irvine
MicroSystems Laboratory have been improving this concept. The basic principle of such a gyroscope is shown in the figure below from Shkel's 2002 patent.[7]
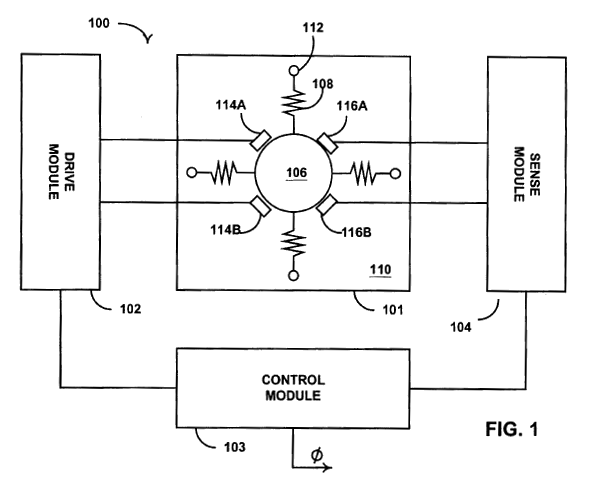
A MEMs gyroscope inspired by the Foucault pendulum. Fig. 1 of US Patent No. 6,481,285 (Andrei M. Shkel and Roger T. Howe, "Micro-machined angle-measuring gyroscope," November 19, 2002; see Ref. 7.)
With reference to the figure, a large central mass (106) is held in place by springs or flextures (108) so that it's free to move in any direction in a plane. The suspension is
isotropic; that is, it has uniform
stiffness in all directions in the gyroscope's plane, just as in a Foucault pendulum. Once the mass is driven to vibrate in a direction, it will continue to vibrate in that direction, even when the chip is rotated. The various sensors and actuators determine the direction of motion and apply a small driving force to keep the mass oscillating.
It all seems so simple; but, as usual,
the devil is in the details, and it's difficult to fabricate such a device. Shkel, along with Igor P. Prikhodko, Sergei A. Zotov and Alexander A. Trusov of the UC Irvine MicroSystems Laboratory have presented a different Foucault pendulum architecture at
The 24th International Conference on Micro Electro Mechanical Systems (MEMS 2011), Cancun, Mexico.[8-11] As shown in the figure, the design has not one, but four proof masses. this
quadrupole version of a Foucault pendulum consists of four symmetrically vibrating tines that are
synchronized by anti-phase
levers.
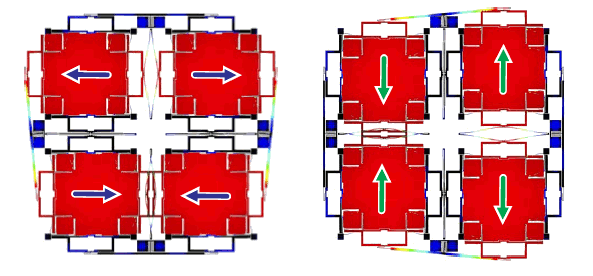
Igor P. Prikhodko, Sergei A. Zotov, Alexander A. Trusov, and Andrei M. Shkel, "Foucault Pendulum On A Chip: Angle Measuring Silicon Mems Gyroscope," MEMS 2011, Cancun, MEXICO, January 23-27, 2011 (To be published).
Because of the symmetry, the vibrational modes in the "X" and "Y" directions are degenerate; that is, they occur at the same frequency. The rotation angle is given by the simple equation,
Θ = arctan(||y||/||x||)
where x and y are the
displacement components. Experimental characterization of this device confirmed linearity in excess of ±450°/sec.
Acknowledgement:
Thanks to
Dr. Alexander A. Trusov, Project Scientist at the UC Irvine
MicroSystems Laboratory, for supplying information on the MEMs quadrapole Foucault Pendulum.
References:
- Umberto Eco, "Foucault's Pendulum," Mariner Books (March 5, 2007, Paperback of original 1988 release), 640 pages, via Amazon
- The Name of the Rose, 1986, Jean-Jacques Annaud, Director (via Internet Moview Database).
- Boris Thiolay, "Le pendule de Foucault perd la boule," Lexpress.fr, April 28, 2010.
- Cleon Teunissen, "The Foucault pendulum - Prelude". Cleon has an extensive web site about the physics of rotation located at http://www.cleonis.nl/.
- R. E. Gillmor, "Gyroscope And Gyroscopic Compass," US Patent No. 1,986,807 (Jan 8, 1935).
- Piyush K. Gupta and Craig E. Jenson, "Rotation rate sensor with center mounted tuning fork," US Patent No. 5,396,144 (Mar 7, 1995).
- Andrei M. Shkel and Roger T. Howe, "Micro-machined angle-measuring gyroscope," US Patent No. 6,481,285 (November 19, 2002).
- Igor P. Prikhodko, Sergei A. Zotov, Alexander A. Trusov, and Andrei M. Shkel, "Foucault Pendulum On A Chip: Angle Measuring Silicon Mems Gyroscope," MEMS 2011, Cancun, MEXICO, January 23-27, 2011 (To be published).
- Alexander A. Trusov, "Investigation of Factors Affecting Bias Stability and Scale Factor Drifts in Coriolis Vibratory MEMS Gyroscopes," Ph.D. Dissertation, University of California,Irvine, 2009 (7.5 MB PDF File).
- Alexander A. Trusov, Adam R. Schofield and Andrei M. Shkel, "Micromachined Tuning Fork Gyroscopes With Ultra-High Sensitivity And Shock Rejection," US Patent Application Number 12/796,452 (Publication Number, US 2010/0313657 A1), June 8, 2010
- Neil Savage, "A Foucault Pendulum on a Chip," IEEE Spectrum, February, 2011.
- Web Site of the 24th International Conference on Micro Electro Mechanical Systems (MEMS 2011), Cancun, Mexico, January 23 - 27, 2011; Preliminary Program (PDF File).
Permanent Link to this article
Linked Keywords: Umberto Eco; Foucault's Pendulum; The Name of the Rose; Sean Connery; semiotics; National Public Radio; NPR; Earth; vanity publication services; conspiracy theories; coded messages; manuscripts; alchemy; ectoplasm; Musée des Arts et Métiers; Foucault; Paris Observatory; proof of concept; Paris Panthéon; latitude; absolute space; technologist; Earth's gravity; chuck; lathe; gyroscope; Global Positioning System; GPS; spacecraft; magnetism; ring laser gyroscope; fiberoptic gyroscope; Sagnac effect; phase; microelectromechanical systems; MEMs; MEMs gyroscope; accelerometer; derivative; US Patent No. 5,396,144; tuning fork; Coriolis force; torsional force; Andrei M. Shkel; University of California (Irvine); MicroSystems Laboratory; US Patent No. 6,481,285; isotropic; stiffness; the devil is in the details; The 24th International Conference on Micro Electro Mechanical Systems (MEMS 2011); quadrupole; synchronization; lever; displacement; Alexander A. Trusov; MicroSystems Laboratory.