A Younger Man's Game?
May 2, 2014
It's often thought that
mathematics is a younger man's game.
English mathematician,
number theorist, and sponsor of
Ramanujan,
Godfrey Harold "G. H." Hardy (1877-1947), expressed this idea obliquely in his "
A Mathematician's Apology." A more direct quotation of his was recalled by
Freeman Dyson,
"Young Men should prove theorems, old men should write books."[1]

A cartoon from Randall Munroe's xkcd Comics, licensed under a Creative Commons Attribution-NonCommercial 2.5 License)
In supposed confirmation of this idea, the usual evidence is cited.[2] This includes the 19th century French mathematician,
Évariste Galois, who formulated
group theory by age twenty, and the 19th century
Norwegian mathematician,
Niels Henrik Abel, who developed
Abelian functions before his death at age 26. Since
theoretical physics is mostly mathematics, we might include
Albert Einstein, who proved
E = mc2 at age 26.
counterexamples are an important part of mathematics, and it's in the counterexamples that we see that the "younger man" principle is flawed.
Andrew Wiles, who published his
proof of Fermat's Last Theorem[3] in 1995 with an assist from
Richard Taylor, was more than forty at the time.
There's the further example of
Russian mathematician,
Grigori Perelman, who was 43 when his proof of the
Poincaré conjecture was certified by the
Clay Mathematics Institute. We can also cite
Paul Erdos, who was a prolific mathematician through the time of his death at age 83. Erdos was awarded the
Wolf Prize at age seventy.

The "Elders" of contemporary mathematics, Andrew Wiles (left), and Grigori Perelman (right). (Left image, copyright C. J. Mozzochi, Princeton N.J., via Wikimedia Commons. Right image by George M. Bergman, via Wikimedia Commons)
One fact that favored important mathematical discoveries by younger mathematicians in earlier times is that there was a smaller
corpus of mathematics that was needed to be learned before practicing the subject. Even today, a mathematician with a freshly minted
Ph.D.. can hit the ground running, since life-long
experience in the field doesn't really help. This is in contrast with the
sciences, especially when
experiment is concerned, where experience is quite important. Older
scientists don't enter as many blind alleys as those younger.
My own concept of a scientist's career, as verified by my own career, is summarized in the following graph in which
productivity is a product of experience and the effort expended.
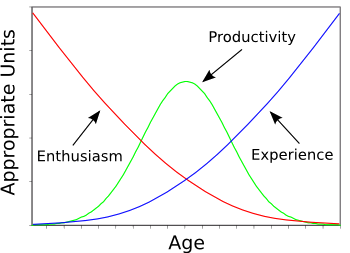
Youthful enthusiasm can produce results only when informed by experience.
The peak location and width varies among individuals.
(Graphed using Gnumeric.)
It's become more difficult to make a
Nobel Prize worthy
scientific discovery. A hundred years ago,
Ernest Rutherford and his
colleagues were making fundamental discoveries in
particle physics with
string and
sealing wax. As
Richard Reeves wrote in his
biography of Rutherford, when one of Rutherford's students needed a
metal tube for an experiment, Rutherford got it by cutting a piece from the
handlebar of an old
bicycle.[4] Today, Nobel-class discoveries in particle physics are made with the
Large Hadron Collider, which cost nearly ten billion
dollars.
Rudolf Mössbauer discovered the
Mössbauer Effect in 1957, when he was just 28 years old. Mössbauer shared the 1961
Nobel Prize in Physics with
Robert Hofstadter. His young age stands in sharp contrast to the ages of today's science
Nobel Laureates.
Santo Fortunato of
Aalto University (Finland) has published a short article in a recent issue of
Nature in which he examines the trend to older Nobel Laureates.[5-6] This effect arises from an increasing time between discovery and the prize award, which has become more than twenty years in many cases. Fortunato writes that some candidates might not live long enough to collect the prize if the trend continues.
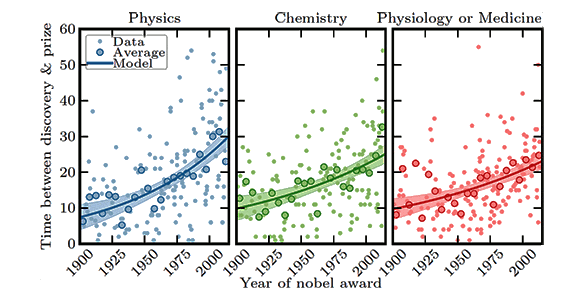
From its inception, the time delay between discovery and prize award has, on average, more than doubled in the scientific fields. (Aalto University image.)[6)]
In a
recent article (Neutrino Mass, March 5, 2014) I wrote how
Frederick Reines (1918-1998) and
Clyde Cowan Jr (1919-1974) made the first experimental detection of the neutrino in 1956; but, when the
Nobel Prize in Physics was awarded for the discovery in 1995, Cowan was long deceased.
Prior to 1940, just 11% of
physics, 15% of
chemistry, and 24% of
physiology or
medicine prizes were awarded more than twenty years after the discovery. By 1985, these percentages had grown to 60%, 52% and 45%. As the graph shows, there's some evidence that the average waiting times are increasing
exponentially.
References:
- D J Albers, "Freeman Dyson: Mathematician, Physicist, and Writer," The College Mathematics Journal, vol. 25, no. 1 (January, 1994).
- Jordan Ellenberg, "Is Math a Young Man's Game?" Slate, May 16, 2003.
- Fermat's Last Theorem is simply stated: There are no positive integers a, b, and c that satisfy an + bn = cn when n>2.
- Richard Reeves, "A Force of Nature: The Frontier Genius of Ernest Rutherford," W. W. Norton, December 3, 2007, 208 pp. (via Amazon).
- Santo Fortunato, "Prizes: Growing time lag threatens Nobels," Nature, vol. 508, no. 7495 (April 10, 2014), p. 186.
- Nobel prize candidates wait often over 20 years to win their prize, Aalto University Press Release, April 11, 2014.
Permanent Link to this article
Linked Keywords: Mathematics; English; mathematician; number theory; number theorist; Srinivasa Ramanujan; Godfrey Harold "G. H." Hardy (1877-1947); A Mathematician's Apology; Freeman Dyson; xkcd comic no. 447; xkcd Comics; Creative Commons Attribution-NonCommercial 2.5 License; 19th century; French; Évariste Galois; group theory; Norwegian; Niels Henrik Abel; Abelian functions; theoretical physics; Albert Einstein; mass-energy equivalence; E = mc2; counterexample; Andrew Wiles; proof of Fermat's Last Theorem; Richard Taylor; Russian; Grigori Perelman; Poincaré conjecture; Clay Mathematics Institute; Paul Erdos; Wolf Prize; Andrew Wiles; Grigori Perelman; Wikimedia Commons; corpus; Doctor of Philosophy; Ph.D.; experience; science; experiment; scientist; productivity; enthusiasm; Gnumeric; Nobel Prize; scientific discovery; Ernest Rutherford; colleague; particle physics; string; sealing wax; Richard Reeves; biography; metal; tube; handlebar; bicycle; Large Hadron Collider; dollar; Rudolf Mössbauer; Mössbauer Effect; Nobel Prize in Physics; Robert Hofstadter; Nobel Laureate; Santo Fortunato; Aalto University (Finland); Nature; Frederick Reines (1918-1998); Clyde Cowan Jr (1919-1974); Nobel Prize in Physics; physics; chemistry; physiology; medicine; Richard Reeves, "A Force of Nature: The Frontier Genius of Ernest Rutherford," W. W. Norton, December 3, 2007, 208 pp.