P = NP
June 9, 2014
By your many years of attempting to impress your
professors, you've learned the art of
cocktail party conversation. Masters of this art will be able to talk grandly on most topics up to a limit of about a minute, at which time the conversation has hopefully changed subject. It's much more
entertaining than just talking about the
weather.
Things are a little harder when you're talking among your
scientific peers, whose depth of
knowledge transcends that of the typical
Sangria sipper. In that case, you meed to haul out the big guns. Among
computer people, a casual mention of the
Entscheidungsproblem is usually all you need to gain your listener's respect without worrying about follow-up questions. It's a subject of which everyone has heard, because of its
historical significance and association with
Alan Turing, but very few have actually studied.
Since the early center of
science and
mathematics was
Europe, including
Germany, many fundamental problems have
German names. These range from the simple
Aufbauprinzip (Aufbau principle) to the tongue-twisting Entscheidungsproblem. This might be expected from a country where the
research foundation is called
Deutsche Forschungsgemeinschaft.
The "halting problem," as it's known in
English, is a
computer science version of the
cinema scientist's lament that "there are things that Man was not meant to know." Possibly the best statement of the halting problem was written in 1935 by
mathematician,
Alonzo Church, who was considering what it means for a
function to be
calculable. He decided that the function would contain an
algorithm, and you would know when the algorithm terminated; that is, the algorithm yields an answer.
In computer science terms, this means knowing that your
program, for a particular input, will eventually halt, or goes on forever. Alan Turing, in his 1937 paper, "
On Computable Numbers With an Application to the Entscheidungsproblem," addressed the problem by first constructing a universal computer, his
Turing machine. He proved that it wasn't possible to decide whether a program on such a machine will halt, effectively proving that there are things that computer scientists are not meant to know.

A physical Turing machine, built by Mike Davey.
You can see its operation in a YouTube video.
(Photograph by "GabrielF," via Wikimedia Commons.
Click for larger image.)
Deciding which problems are too hard to tackle is one task of an effective scientist. He might not know that his research will lead to a dead end, but the
referees of his
research proposal likely will. The halting problem notwithstanding, computers have been successfully performing many of our
calculations for years. Despite these successes, there are some calculations that are very difficult.
One simple example of such a problem (simple enough to be presented in the
cartoon shown below) is the
subset sum problem. If you have a
set of
numbers, is it possible for members of the set to
add to a particular number? There's no algorithm to do this; and, if you have many numbers in the set, you need to try a lot of combinations to see whether it's possible.

A cartoon from Randall Munroe's xkcd Comics, licensed under a Creative Commons Attribution-NonCommercial 2.5 License. (xkcd comic 287.)
The complexity of this calculation increases at a rate that's not known to be polynomial in
time; that is, it's "
nondeterministic polynomial" (NP) in time. Verification of the answer happens in
polynomial time (P). A polynomial execution time for calculations involving N elements would be something like N
1, N
2, or N
3, and so on. NP execution, however, would be something like 2
N, which becomes very large for large N.
It would be nice if every problem with a quickly verified solution would have an algorithm that allows its quick computation as well. In the language of computer science, we would like to have P=NP, rather than the
converse, P≠NP. This
P vs NP problem is an
open problem that's important enough to have been designated one of the seven, million dollar,
Millennium Prize Problems selected by the
Clay Mathematics Institute. Its solution would be important to such diverse areas as
cryptography and
economics.
Public key cryptography involves the idea that it's easy to
multiply two huge
prime numbers to get an even larger number, but it's very difficult to
factor that large number into its prime components. The factoring is NP. Nearly every NP problem is
NP-complete, a
terminology expressing the fact that a polynomial solution of any one of those can be easily applied to the rest.[1] The traveling-salesman problem, which I wrote about in a
previous article (The Traveling Salesman Problem, March 1, 2013), is NP-complete.
The problem expressed in the above cartoon is NP-complete, but there are so few elements that the solution can be found by inspection, or just a few computer calculations. When the cartoonist,
Randall Munroe, created the cartoon, he didn't realize that the problem had more than one solution.[2] These are seven mixed fruit orders and the combination of one order of mixed fruit, two orders of hot wings, and one sampler plate. One web site has a few elegant programs for the
efficient solution of this particular problem.[3]
My computer solution is not at all
elegant, although it is very general. I used a the
Monte Carlo method, and you can view my
C language source code,
here. In the Monte Carlo method, you try
random combinations of multiples of the items until you find one that works. There's some
method to the madness, since you purposely don't select multiples of any one item that will go over the limit ($15.05, in this case), as shown in the table.
| Item | Maximum Number |
| Mixed Fruit | 7 |
| French Fries | 5 |
| Side Salad | 4 |
| Hot Wings | 4 |
| Mozzarella Sticks | 3 |
| Sampler Plate | 2 |
So, how well does this approach work? As can be seen in the
histogram, the program often finds a solution after just a few random selections. If you just multiply the maximum numbers in the table, you get 3360, so you should expect to find a solution somewhat close to that number of random selections, if a solution exists. You'll note, also, that there are still cases for which a solution is found at our patience limit, which was 30,000 random selections.
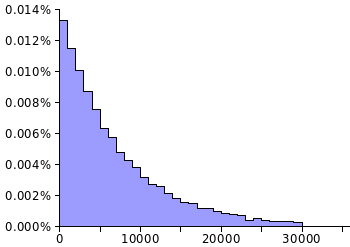
Histogram of the number of random selections required to get a Monte Carlo solution to xkcd cartoon 287.
30,000 trials were attempted.
(Gnumeric.)
![]()
References:
- Larry Hardesty, "Explained: P vs. NP," MIT News Office, October 29, 2009.
- Explain 287: NP-Complete, Explain xkcd Web Site.
- Solving the NP-complete problem in XKCD, Stack Overflow Web Site.
Permanent Link to this article
Linked Keywords: Professor; cocktail party; conversation; entertainment; entertaining; weather; science; scientific; peer; knowledge; Sangria; computer scientist; computer people; halting problem; Entscheidungsproblem; history; historical; Alan Turing; science; mathematics; Europe; Germany; German language; Aufbau principle; Aufbauprinzip; research; foundation; Deutsche Forschungsgemeinschaft; English language; computer science; film; cinema; scientist; lament; mathematician; Alonzo Church; function; calculation; calculable; algorithm; computer programming; program; On Computable Numbers With an Application to the Entscheidungsproblem; Turing machine; Mike Davey; YouTube video; Wikimedia Commons; peer review; referee; research proposal; cartoon; subset sum problem; set; number; addition; NP Complete, xkcd comic no. 287; Randall Munroe; xkcd Comics; Creative Commons Attribution-NonCommercial 2.5 License; polynomial; time; nondeterministic polynomial; polynomial time; converse; P vs NP; open problem; Millennium Prize Problem; Clay Mathematics Institute; cryptography; economics; public key cryptography; multiplication; multiply; prime number; factorization; factor; NP-complete; terminology; traveling salesman; efficiency; efficient; elegance; elegant; Monte Carlo method; C programming language; source code; randomness; random; method to the madness; histogram; Gnumeric.