| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Georg Ohm and Ohm's Law
March 15, 2013
Tomorrow,
March 16, is the
anniversary of the birth of
Georg Simon Ohm, discoverer of what's now called
Ohm's law. Ohm, who was born on March 16, 1789, was a
German high school teacher when he performed the
experiments demonstrating that the
electrical voltage E across a
conductor increases in proportion to the applied
current I. The
proportionality constant is the
resistance R, now measured in
ohms; viz,
E = I R
Ohm may have inherited his facility for experiment from his father, who was a
locksmith. Ohm's family valued education, and his younger brother,
Martin, became a
mathematician. Ohm studied mathematics on his own while he worked as a
private tutor in
Neuchâtel. His private study paid off. Quitting
Switzerland, Ohm entered the
University of Erlangen, and he received a
Ph.D. in
mathematics on October 25, 1811, just a few months after his arrival.
Ohm's law illustrated graphically as Georg Ohm equals Alessandro Volta over André-Marie Ampère.
(Source images, Ohm, Volta, and Ampère, from Wikimedia Commons.)
Ohm served as a
lecturer in mathematics at the university for a time at very little pay. Short on cash, he re-purposed himself as a high school mathematics teacher in
Bavaria, and he taught briefly at two public schools. Ohm knew this was not the life for which he had hoped, so he spent time writing a
geometry textbook, the
manuscript of which he sent to
King Frederick Wilhelm III of Prussia.
The king was suitably impressed, and this landed Ohm a better teaching position at the
Jesuit Gymnasium of
Cologne (another high school) in the Fall of 1817. At this school, Ohm taught
physics as well as mathematics, and the school had an excellent physics
laboratory for the time. It was here that Ohm did his electrical experiments, which were summarized in the 1827 paper, "The Galvanic Circuit Investigated Mathematically," (Die galvanishe Kette, mathematisch bearbeitet).
Publication of what's now called "Ohm's Law" probably assisted Ohm in gaining a position at the Polytechnic School of
Nuremberg in 1833, and his becoming a
professor of experimental physics at the
University of Munich in 1852.
The resistor is one of the three (
perhaps four) fundamental electrical components, the others being the
capacitor and
inductor. The figure below shows the
electrical symbol for a resistor, and how to calculate the equivalent resistance when resistors are connected in
series and
parallel.
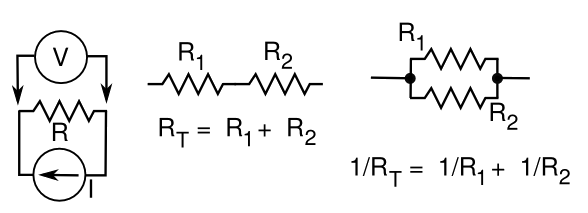
Ohm's law illustrated using conventional electronic component symbols (left), and the equivalent resistance of series (middle) and parallel (right) combinations of resistors. (Illustration by the author using Inkscape.)
The series and parallel resistance formulas are easy to understand when you relate them to the fundamental physics of resistance. The resistance
R of a uniform
rod or
bar of a
material with
resistivity ρ, cross-sectional area
A and length
L, as shown in the figure, is just
R = ρ (L/A)
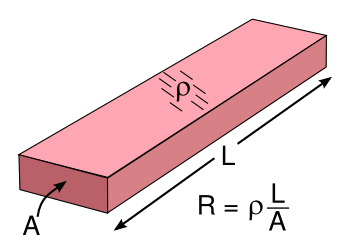
Resistance formula for a conductor with resistivity, ρ.
(Illustration by the author using Inkscape.)
You can see that when you put resistors in series, you add the virtual lengths of their internal conductors, so the series formula is obvious. In the parallel case, you're adding the cross-sectional areas, so the math is a little different. You're adding the
conductance, which is the
reciprocal of the resistance.
All this is textbook stuff, which is exciting to just a few students. There are combinations of resistors which are much more interesting, such as the
infinite lattice of resistors shown in the figure. Whenever the idea of infinity enters a problem, it becomes more interesting and often more complex.
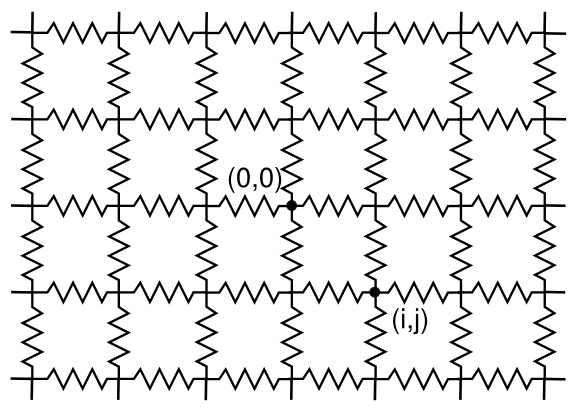
An infinite lattice of resistors in two dimensions. Measurements between some nodes will give an experimental value of pi (π). (Illustration by the author using Inkscape.)
A very nice analysis of this infinite array of resistors was published fifteen years ago,[1] and there have been quite a few papers on this lattice array, similar lattice arrays, and cubic arrays.[1-8]
The following table shows the calculated resistance values, in units of the identical resistance values in the array, between the origin (0,0) and some nearby lattice nodes.[1] The origin, of course, can be anywhere, since this is an infinite array.
| (i,j) | R | |
(i,j) | R |
| 0,0 | 0 | |
2,2 | (8/3π) |
| 0,1 | 1/2 | |
3,3 | (46/15π) |
| 1,0 | 1/2 | |
4,4 | (352/105π) |
| 1,1 | 2/π | |
5,5 | (1126/315π) |
The interesting thing here is that some nodes will give
rational numbers, and other nodes will give values containing
π, an
irrational,
transcendental number.
References:
- D. Atkinson and F. J. van Steenwijk, "Infinite resistive lattices," Amer. Jour. Phys., vol. 67, no. 6 (June, 1999), pp. 486-492. A PDF copy can be found, here.
- J. H. Asad, "Infinite Body Centered Cubic Network of Identical Resistors," Arxiv Preprint Server, February 19, 2013.
- Jihad H. Asad, "Exact Evaluation of The Resistance in an Infinite Face-Centered Cubic Network," Arxiv Preprint Server, October 7, 2012.
- J. H. Asad, "Infinite Face Centered Cubic Network of Identical Resistors," Arxiv Preprint Server, May 5, 2012.
- Jozsef Cserti, Gabor Szechenyi and Gyula David, "Uniform tiling with electrical resistors," Arxiv Preprint Server, March 7, 2011.
- J. H. Asad, R. S. Hijjawi, A. J. Sakaji and J. M. Khalifeh, "Resistance Calculation for an infinite Simple Cubic Lattice- Application of Green's Function,"Arxiv Preprint Server, May 1,2009.
- J. H. Asad, A. J. Sakaji, R. S. Hijjawi and J. M. Khalifeh, "On the resistance of an Infinite Square Network of Identical Resistors- Theoretical and Experimental Comparison," Arxiv Preprint Server, April 3, 2009.
- R. S. Hijjawi, J. H. Asad, A. J. Sakaji, M. Al-Sabayleh and J. M. Khalifeh, "Infinite Simple 3D Cubic Lattice of Identical Resistors (Two Missing Bonds)," Arxiv Preprint Server, March 24, 2009.
Permanent Link to this article
Linked Keywords: March 16; birthday; anniversary of the birth; Georg Simon Ohm; Ohm's law; Germany; German; high school; teacher; experiment; electrical voltage; electrical conductor; electric current; proportionality constant; resistance; ohm; locksmith; Martin Ohm; mathematician; private tutor; Neuchâtel; Switzerland; University of Erlangen; Doctor of Philosophy; Ph.D.; mathematics; Alessandro Volta; André-Marie Ampère; Wikimedia Commons; lecturer; Bavaria; geometry; textbook; manuscript; King Frederick Wilhelm III of Prussia; Jesuit; Gymnasium; Cologne; physics; laboratory; Nuremberg; professor; University of Munich; memristor; capacitor; inductor; electronic symbol; electrical symbol; series and parallel circuits; Inkscape; rod; bar; material; resistivity; conductance; multiplicative inverse; reciprocal; infinity; infinite; lattice; node; pi; rational number; irrational number; transcendental number.