| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
The S-Curve
August 1, 2011
Many things in
nature and
human culture follow an "S"-shaped development. The curve that describes this is usually known as the
S-curve, or
sigmoid function. Things start slowly, they accelerate quickly after a time, and then they
saturate. The
logistic function, the most used sigmoid function, is easily written and calculated,
S(t) = 1/(1 + e-t)
in which
S(t), the sigmoid function of
t, as can be seen in the graph below, ranges from zero to one. The
independent variable is usually named
t, since most references to the function refer to time. A time
t = 0 specifies when we're halfway up the curve. The units of
t can be scaled so that it makes sense in a given problem, so we can write
kt instead of
t.
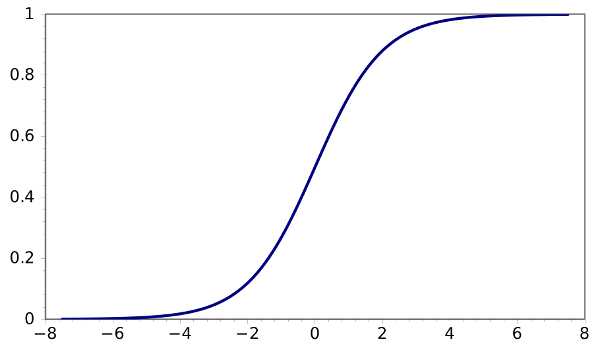
The sigmoid function, 1/(1+exp(-t)). Graph via Gnumeric.
One example of the S-curve in action, the technology S-curve, should be familiar to readers of this blog. It all starts with an
invention, when a barely functional device is produced. As development continues, the performance reaches an acceptable level, and continued development hones the invention into a useful gadget. Finally, no matter how hard you try, you can't make significant improvement, so progress stops. This process can be summarized, as follows:
Invention -> Technology Improvement -> Mature Technology -> Aging Technology
For argument's sake, the transition points between these stages can be considered to be at S(t) = 0.05, 0.75 and 0.95. In economics, the process is known as the
diffusion of innovations. Examples in
economics are provided by Arnulf Grübler, who showed that the spread of large
capital projects, such as
canals,
railroads and
highways, follows the S-curve.[1]
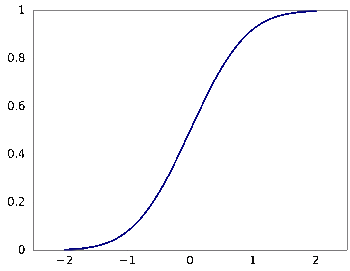
The cumulative distribution function, (1/2)(1+erf(t)), where erf() is the error function.
The cumulative distribution function has a sigmoid shape.
Graph via Gnumeric)
Explanation of the S-curve in such human activities is relatively easy, if you posit certain actions, but its appearance in some natural processes is harder to explain.
Adrian Bejan of the
Department of Mechanical Engineering and Materials Science,
Duke University, and Sylvie Lorente of the Laboratoire Matériaux et Durabilité des Constructions,
Université de Toulouse, have published a paper in a recent issue of the
Journal of Applied Physics (JAP) in an attempt to bring all sigmoid processes under a single umbrella
hypothesis. Their hypothesis concerns
flow.[2-4]
Flow has been considered to be an important physical principle since the time of the
Greek philosopher,
Heraclitus of Ephesus (c. 500 BC). Heraclitus' philosophy is usually summarized by the expression,
Παντα ρει (Everything flows), that Heraclitus did not himself say. This expression is contained in the
logo for the
The Society of Rheology, and rheology, of course, is the science of flow.
Heraclitus in Raphael's School of Athens.
Heraclitus, who was always described as a rather morose figure, sits apart from the other philosophers.
Raphael drew the image of Heraclitus to resemble Michelangelo.
(Via Wikimedia Commons))
Heraclitus was a fount of interesting ideas. The main point of his philosophy is that change is inevitable, as expressed in several of his many sayings; viz.,
"Ever-newer waters flow on those who step into the same rivers." (More colloquially, "You can't step twice in the same river twice.")
"All things move and nothing remains still."
In their JAP paper, Bejan and Lorente see an
analogy of "S"-curve phenomena and how flow systems modify their designs over time to continue their flow in the face of
friction and other obstacles. Bejan first posited his flow principle about fifteen years ago, and he's been developing it ever since.[3] To quote from their paper, "For a finite size flow system to persist in time (to live), its configuration must evolve such that it provides easier and easier access to its currents."[2]
The essential point of the model is that flow systems start with direct
channels, but these channels branch over time. The initial channels penetrate the region quickly, but it's then necessary to access slower flows from branches. Eventually, when the branching mechanism extends as far as it can, flow reaches a maximum. The paper has a few descriptive equations, but this is more of a concept, an analogy, than an easily applied model.
One interesting example used in the paper involves
petroleum extraction. Early wells had a single pipe in the ground, and that evolved to oil fields with many pipes in the ground. Now, as illustrated in one figure of their paper, oil well piping has underground branches that resemble a river with
tributaries.[2] The research was supported by the
National Science Foundation, the
U.S. Air Force Office of Scientific Research and the
National Renewable Energy Laboratory.[3]
References:
- Arnulf Grübler, "The Rise and Fall of Infrastructures: Dynamics of Evolution and Technological Change in Transport," International Institute for Applied Systems Analysis (1999), 305 pages. A PDF file appears to be available here.
- A. Bejan and S. Lorente, "The constructal law origin of the logistics S curve," Journal of Applied Physics, vol. 110, no. 2 (July 20, 2011), Document No. 024901 (4 pages)
- Richard Merritt, "Seeing the S-Curve in Everything, " Duke University Press Release, July 20, 2011.
- YouTube video: Adrian Bejan describes the constructal theory of generation of design in nature at Bucharest Conference.
Permanent Link to this article
Linked Keywords: Nature; human culture; S-curve; sigmoid function; saturation; logistic function; independent variable; Gnumeric; invention; diffusion of innovations; economics; capital; canal; railroad; highway; cumulative distribution function; error function; Adrian Bejan; Department of Mechanical Engineering and Materials Science; Duke University; Université de Toulouse; Journal of Applied Physics; hypothesis; flow; Greek; philosopher; Heraclitus of Ephesus; Panta rhei; Παντα ρει; Everything flows; logo; The Society of Rheology; Raphael's School of Athens; Raphael; Michelangelo; Wikimedia Commons; analogy; friction; channel; petroleum extraction; tributary; National Science Foundation; U.S. Air Force Office of Scientific Research; National Renewable Energy Laboratory; Arnulf Grübler; The Rise and Fall of Infrastructures: Dynamics of Evolution and Technological Change in Transport.