| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Carbon Nanotube Capillarity
September 6, 2011
Capillary action, or capillarity, is a very useful physical phenomenon. I mentioned capillarity in the context of
heat pipes in a
previous article (Pumping Water, August 10, 2010).
A heat pipe is a passive device that uses the
surface tension effect between
liquids and
solids, also known as capillarity, to transport
heat. The liquid extracts heat by
boiling, the vapors migrate to a part of the heat pipe that's below the
boiling point, where they condense, and the liquid is drawn back to the hot zone via capillarity in a
wicking material.
In a blatant use of the
rhetorical ploy called
ad auctoritatem, I'll mention that one of
Einstein's first papers (Folgerungen aus den Capillaritätserscheinungen, 1901) was about capillarity.[1] As I wrote in a
recent article (Trees, Wooden Variety, July 27, 2011), tall trees use capillarity to raise
water to heights beyond the thirty
foot limit of
suction pumps.
Capillary action will lift water in a tube of inside radius
r to an approximate height
h given by
h = (1.4 x 10-5)/ r
where
h and
r are in the same units. A tube of one
micrometer radius will raise water to a height of about 14
meters, and the equation asserts wonderful things for smaller radii. In reality, how small can we make a tube and still get water to suck up into it?
Scientists have taken the problem to an extreme by showing that
water spontaneously flows into
carbon nanotubes.[2-4] This is unexpected, since a cursory analysis of what should happen when water is confined at these near
atomic scale dimensions indicates that
entropy and
bonding should both decrease; that is, water really shouldn't get sucked into nanotubes.
To discover why it happens, scientists at
Caltech used
molecular dynamics simulations of water confined in 0.8 to 2.7-nm diameter carbon nanotubes to calculate the entropy,
enthalpy, and
free energy. The simulations show that for all nanotube sizes, the water inside the nanotube is more stable than bulk water. However, the
conformation of the water changes with nanotube size.
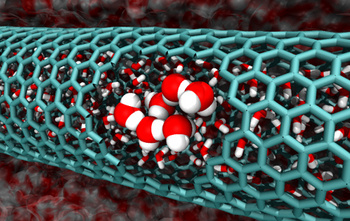
A cutaway simulation of a two nanometer-diameter carbon nanotube with confined water molecules.
(Caltech Image/Tod Pascal))
In small diameter nanotubes (0.8 - 1.0 nm), the water is
vapor-like; for 1.1 - 1.2 nm, the water is
ice-like; and for diameters larger than 1.4 nm, the water is liquid-like.[2] The parameter that's responsible for the stability of water inside carbon nanotubes is the entropy change.
Says
William A. Goddard, Charles and Mary Ferkel Professor of
Chemistry,
Materials Science, and
Applied Physics at Caltech, and director of its
Materials and Process Simulation Center, "It's a pretty surprising result... People normally focus on energy in this problem, not entropy."[3]
The simplistic view is that water, which forms a network of
hydrogen bonds, is very stable, and breaking these hydrogen bonds so that water can flow into the small volume of a nanotube requires
energy. What happens is that the hydrogen bonds in bulk water restrict
molecular motion, so the entropy of bulk water is low. The entropy that water gains by entering the nanotubes is enough to outweigh any energy losses of hydrogen bond breaking. It's energetically favored for water to spontaneously flow into the tubes.
Grave of Ludwig Boltzmann at the Zentralfriedhof (Central Cemetery) of Vienna, Austria
At the top is his famous entropy equation,
S = k log W.
The modern transcription uses Ω instead of W. Both of these letters are mapped to 'W' on the keyboard, so if you mistype, no one will notice.
(Photo by Daderot, via Wikimedia Commons))
The interesting ice-like structure that exists for water inside 1.1 - 1.2 nm diameter nanotubes is the result of a perfect match between the confined space, the arrangement of atoms in the water molecule, and the hydrogen bonding between molecules.[3]
The Caltech team devised a new simulation method, called the two-phase
thermodynamic model, that helped in the entropy calculations. Said Goddard, "The old methods took eight years of computer processing time to arrive at the same entropies that we're now getting in 36 hours."[3] The Caltech team thinks that their research can be used to design
supermolecules for
water purification. A
polymer with the same
pore size as carbon nanotubes could suck water out of solution.[3]
References:
- Albert Einstein, "Folgerungen aus den Capillaritätserscheinungen," Annalen der Physik, vol. 309, no. 3 (1901), pp. 513-523.
- Tod A. Pascal, William A. Goddard and Yousung Jung, "Entropy and the driving force for the filling of carbon nanotubes with water," Proc. Natl. Acad. Sci., vol. 108, no. 29 (July 19, 2011), pp. 11794-11798.
- Kimm Fesenmaier, "Caltech Researchers Find That Disorder Is Key to Nanotube Mystery," Caltech Press Release, August 12, 2011.
- Researchers find disorder is key to nanotube mystery, RD Magazine, August 12, 2011.
Permanent Link to this article
Linked Keywords: Capillary action; heat pipe; surface tension; liquid; solid; heat; boiling; boiling point; wicking material; rhetoric; argumentum ad verecundiam; ad auctoritatem; Albert Einstein; water; foot; suction; micrometer; meter; scientist; carbon nanotube; atom; atomic; entropy; chemical bond; bonding; California Institute of Technology; Caltech; molecular dynamics simulation; enthalpy; free energy; chemical structure; conformation; Tod Pascal; steam; vapor; ice; William A. Goddard; chemistry; materials science; applied physics; Materials and Process Simulation Center; hydrogen bond; energy; molecular; Ludwig Boltzmann; Vienna, Austria; Wikimedia Commons; thermodynamics; macromolecule; supermolecule; water purification; polymer; porosity; pore size; Folgerungen aus den Capillaritätserscheinungen.